- #1
regisz90
- 19
- 0
We have two groups measuring the same resistors, the nominal value is unknown. Group 1 is slower and because of that they did not calcute the s1 empirical standard deviation.
We have to give the confidence interval for the nominal value of the resistance at confidence level p=90% and prove that this is the right way to calculate it.
Somewhere i found an answer, but i don't really understand why is it correct and also i need to prove that its right.
The solution was this: "Even if we don't know s1, we can use estimator R1, because its more accurate than R2 (because of the larger amount of information). However we can only use s2 empirical standard dev. and the confidence interval should be calculated by student´s-t distribution with degree of freedom N2-1=19"
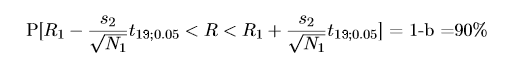
The s2 is divided by root square of N1 however the student´s distribution has degree of freedom N2. Can someone explain me, why is this correct, why can we combine the two measurements this way or better show me the deduction?
- Group 1: N1=500 , R1=6903 , s1=unknown
- Group 2: N2=20 , R2=6880 , s2=168.3
We have to give the confidence interval for the nominal value of the resistance at confidence level p=90% and prove that this is the right way to calculate it.
Somewhere i found an answer, but i don't really understand why is it correct and also i need to prove that its right.
The solution was this: "Even if we don't know s1, we can use estimator R1, because its more accurate than R2 (because of the larger amount of information). However we can only use s2 empirical standard dev. and the confidence interval should be calculated by student´s-t distribution with degree of freedom N2-1=19"
The s2 is divided by root square of N1 however the student´s distribution has degree of freedom N2. Can someone explain me, why is this correct, why can we combine the two measurements this way or better show me the deduction?