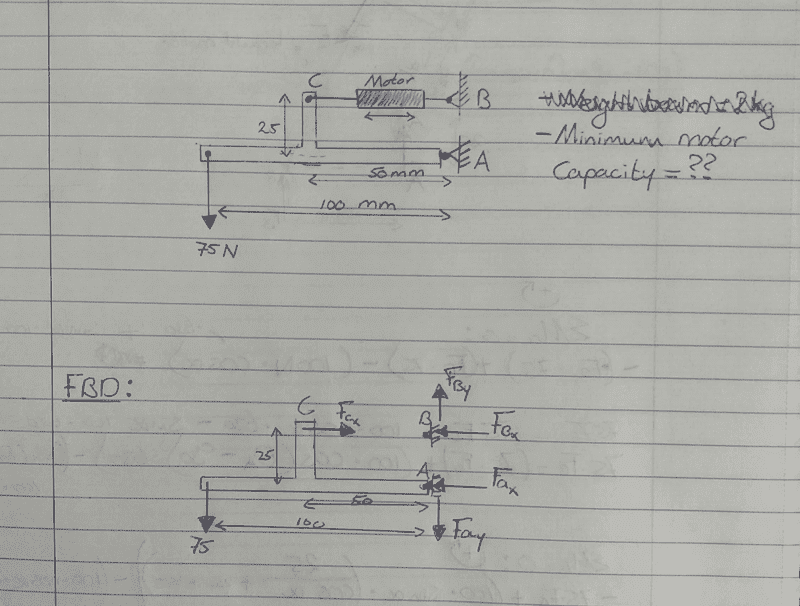
To keep it simple, say you have only your 75 N force, moving at 5 m/s.
Doing a sum of moments about point
A will give a horizontal force of 300 N at point
C (basically, ##75\ N \times \frac{100\ mm}{25\ mm} = 300\ N##).
To find the horizontal velocity at point
C , you first find the velocity at point
C. The center of rotation is point
A, thus the angular velocity is ##\frac{5000\ mm/s}{100\ mm} = 50\ rad/s##. Using the arm length
AC - ##\sqrt{25^2 + 50^2} = 55.9017\ mm## - you can find that the velocity at point
C is ##55.9017\ mm \times 50\ rad/s = 2795\ mm/s## (or 2.795 m/s). That velocity is perpendicular to the arm AC, i.e. at an angle of 26.5651° (##= atan\left(\frac{25\ mm}{50\ mm}\right)##). The horizontal component of that velocity is thus ##2.795\ m/s \times \sin 26.5651° = 1.25\ m/s##.
The power required at point
C (horizontally only) is force times velocity, or 300 N X 1.25 m/s = 375 W. Surprise, surprise, it is the same as 75 N X 5 m/s = 375 W. That is because, in a system, energy cannot be destroyed, it is conserved. Since there is only one input point and one output point, they must be equal.
Now you can add other input forces, such as the frame inertia (frame mass times its acceleration, including gravity) or you can add a http://mechanicsmap.psu.edu/websites/6_friction/bearing_friction/bearingfriction.html at the different pivots. All of these will alter the horizontal force at point
A. But the velocity will remain the same. If you calculated the sum of all these powers from each input point, it would also be equal to the new calculated linear actuator power.
Mech_LS24 said:
The location where the speeds applies doesn't play a role in this?
No, it doesn't because of the
mechanical advantage. When the force increases, the velocity decreases equally (and vice versa).
Mech_LS24 said:
I found one on Amazon (
Linear actuator) and they are referring to the "load capacity" which is capable for 330 lbs. Should this be converted to power? So this linear actuator can handle 330 lbs=1500 N. Makes:
1500 N x 0.5 m/s = 750 Watts. The actuator can produce 750 Watss of power for 0.5 m/s.
On the linked page, it also says that it moves at 5.7 mm/s. This means that its maximum power is 1468 N X 0.0057 m/s = 8.37 W. Not fast enough (< 1.25 m/s) and not powerful enough (< 375 W) for your application.
Mech_LS24 said:
I re-calculated the FBD (see below). Now I find a force acting on the motor of 0 N ??
You shouldn't include forces at point
B in your diagram. Only consider the forces acting on the frame.