Statics - Determine the Reactions on this bent bar levering between two surfaces

[Nova_Chr0n0]

Homework Statement

Determine the reactions at the smooth contact points A, B, and C on the bar.

Relevant Equations

N/A

The figure is shown below:

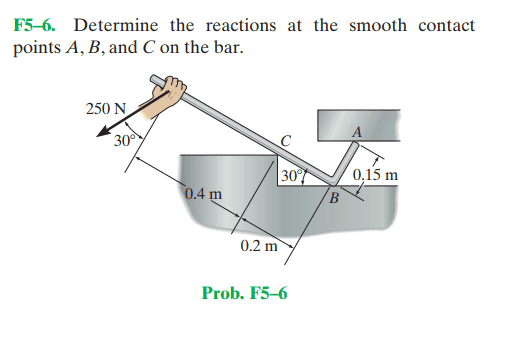
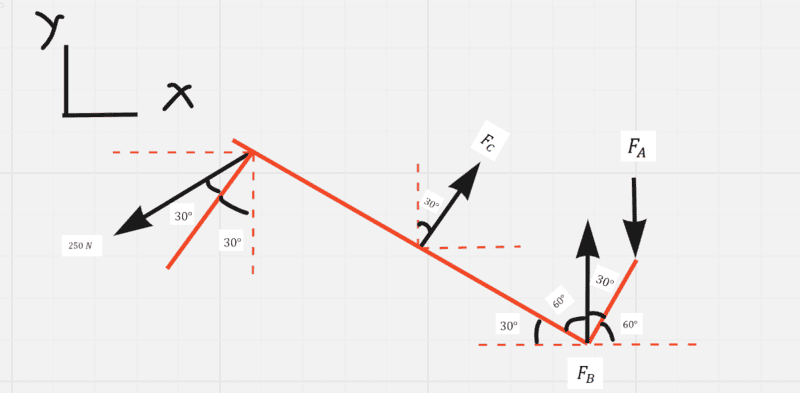
Here is my FBD for the figure with assign +x and +y directions

I started off by summing up the forces in the x-direction:

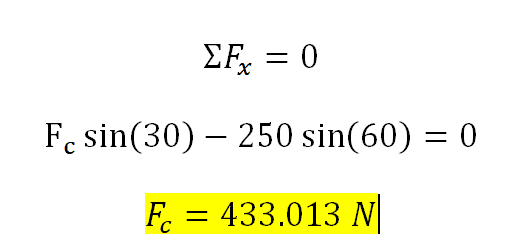
Next is the summing up of the forces in the y-direction:

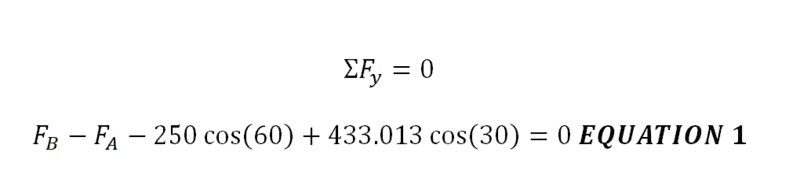
After this, I solved for the moment at point A: assuming that counter-clockwise is +

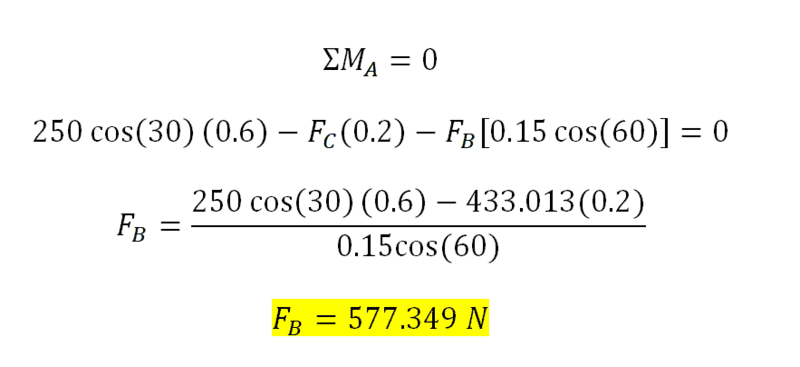
Now from equation 1, if I input the value of F_B, i would get F_A = 827.349 N.

Here is where my question starts. When I tried to search for the problem in the internet to double check the answers that I've got, I only got the Force C right. Mainly because most of them choose B as their moment point. Solution below:

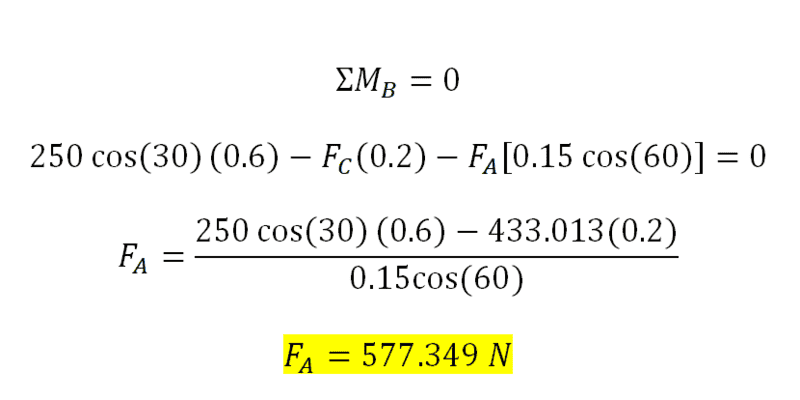
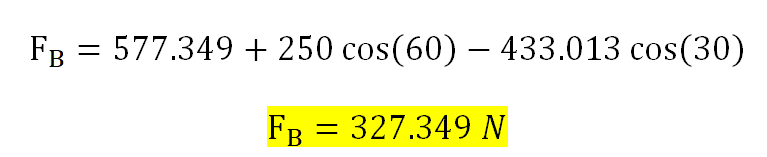
With this, I got two different values for Fa and Fb when choosing the moment point. I tried to find solution in the internet where they choose A as their moment point but I didn't finding anything. I tried to check my solution multiple times but I cannot find my mistake here. Is there something wrong with the values in my solution? Or is it wrong that I decided to choose A as my point of moment?

 

[Chestermiller]

You left out one of the components of the man's force in your moment balance around point A.

 

[Lnewqban]

@Nova_Chr0n0

You have represented the reactions correctly, because surface friction should not be considered ("smooth contact points").
For points A and B, the reactions should be perfectly perpendicular to each flat surface.

For point C, the reaction should be perfectly perpendicular to the bar.

Do you have the full correct response to this problem?
It seems to be a complicated problem the way it is shown.
For stable condition, you either need point C or B, but not both.

Nevertheless, point C seems to be necessary for limiting any sliding of the bar horizontally toward the left.
Perhaps, we should only consider C as a simple horizontal support because of that (otherwise, any vertical reaction in C would need to be subtracted from any vertical reaction in B).

 

[erobz]

@Nova_Chr0n0

You have represented the reactions correctly, because surface friction should not be considered ("smooth contact points").
For points A and B, the reactions should be perfectly perpendicular to each flat surface.

For point C, the reaction should be perfectly perpendicular to the bar.

Do you have the full correct response to this problem?
It seems to be a complicated problem the way it is shown.
For stable condition, you either need point C or B, but not both.

Nevertheless, point C seems to be necessary for limiting any sliding of the bar horizontally toward the left.
Perhaps, we should only consider C as a simple horizontal support because of that (otherwise, any vertical reaction in C would need to be subtracted from any vertical reaction in B).

To me it seems the reaction at B is (should be) zero.

 

[Nova_Chr0n0]

You left out one of the components of the man's force in your moment balance around point A.

Thank you very much! I didn't notice that I left out the component force of 250 N that is parallel to the bar. I've now gotten the same answer.

 

[Nova_Chr0n0]

@Nova_Chr0n0

You have represented the reactions correctly, because surface friction should not be considered ("smooth contact points").
For points A and B, the reactions should be perfectly perpendicular to each flat surface.

For point C, the reaction should be perfectly perpendicular to the bar.

Do you have the full correct response to this problem?
It seems to be a complicated problem the way it is shown.
For stable condition, you either need point C or B, but not both.

Nevertheless, point C seems to be necessary for limiting any sliding of the bar horizontally toward the left.
Perhaps, we should only consider C as a simple horizontal support because of that (otherwise, any vertical reaction in C would need to be subtracted from any vertical reaction in B).

The solution that is at the last page of the e-book I've got (Mechanics - Hibeller 14th edition) also used moment at B. Here is its solution:

But I've already got the correct solution, as Sir Chestermiller stated that I've left out one force.

 

[erobz]

It may be the solution in the book, but does $N_B$ being non-zero make sense? Is the rod $AB$ compressed when it's placed in between the plates before the force is applied? If so... there is a host of other questions that need resolved before the normal reactions could be determined.

If it was slid into place without force fit (as a rigid body - a pure statics problem), then when the force is applied, point $B$ immediately loses contact with the plate below it.

I think the problem is flawed.

 

[Chestermiller]

It may be the solution in the book, but does $N_B$ being non-zero make sense? Is the rod $AB$ compressed when it's placed in between the plates before the force is applied? If so... there is a host of other questions that need resolved before the normal reactions could be determined.

If it was slid into place without force fit (as a rigid body - a pure statics problem), then when the force is applied, point $B$ immediately loses contact with the plate below it.

I think the problem is flawed.

I don't follow. Can you elaborate. Are you saying that the angle iron could not be placed into its shown position without any forces acting on it?

 

[erobz]

I don't follow. Can you elaborate. Are you saying that the angle iron could not be placed into its shown position without any forces acting on it?

In order to have normal forces at both $B$ and $A$ it would have to be wedged into place. The rod $AB$ would necessarily be compressed - A forced fit.

 

[Chestermiller]

In order to have normal forces at both $B$ and $A$ it would have to be wedged into place. The rod $AB$ would necessarily be compressed - A forced fit.

Can't it be rotated and translated into place?

 

[erobz]

Can't it be rotated and translated into place?

That doesn't help IMO. The rod is rigid (and massless). In order for it to have contact on both sides it would need to be compressed. In the limit as zero clearance is approached, the moment the force was applied ( at the end) , normal force at $B$ would go to zero.

If it the case that the rod $AB$ is compressed then the normal forces are arbitrary at this point without further information detailing the compression, rod material , etc...

 

[Chestermiller]

That doesn't help IMO. The rod is rigid (and massless). In order for it to have contact on both sides it would need to be compressed. In the limit as zero clearance is approached, the moment the force was applied $B$ would go to zero.

Are all the force and moment balances satisfied by the given solution? If so, then I can't see what's wrong. The solution is statically determinate. Could the rod have be put in place if it were slightly deformable?

 

[erobz]

Are all the force and moment balances satisfied by the given solution? If so, then I can't see what's wrong. The solution is statically determinate. Could the rod have be put in place if it were slightly deformable?

The rod without the applied force is statically indeterminant. What are the normal forces on the rod before the load is applied?

 

[erobz]

The following seems ok as a rigid bar statics problem (EDIT: actually, even this is problematic without friction):

The problem as stated is inconsistent with its own assumptions. Sure it yields "an answer", but I don't buy its uniqueness.

 

[Chestermiller]

The following seems ok as a rigid bar statics problem (EDIT: actually, even this is problematic without friction):

View attachment 332094
The problem as stated is inconsistent with its own assumptions. Sure it yields "an answer", but I don't buy its uniqueness.

The following seems ok as a rigid bar statics problem (EDIT: actually, even this is problematic without friction):

View attachment 332094
The problem as stated is inconsistent with its own assumptions. Sure it yields "an answer", but I don't buy its uniqueness.

I defer to you. You seem very confident.

 

[erobz]

You seem very confident.

I'm going to try to make my point once more, assuming I have not been doing that well.

Let's pretend it the rod is in there touching both $A$ and $B$, we don't care how it got there, and we are not yet applying any load to the end.

When we start to apply the load in question to the end, the normal force at $B$ is going to decrease in magnitude, and the normal force at $A$ is going to increase. So if its calculated that $N_B = 327 \rm{N}$ after the load is applied (using pure statics), it has then necessarily decreased from some larger value it previously had at loads between zero and $F$. What value did it have before we applied the load? The only way we can specify that initial value from which it decreased is to specify how much the rod segment $AB$ was initially compressed to get it into the slot (given the properties of the rod). Given a final load of $F$ ( and a rigid bar), the normal force at $B$ must depend on the value it had before the load was applied. The idea that it inexplicably ends at $327 \rm{N}$ whether it was put in into the slot under $0.001 \rm{N}$ of compression or $1000 \rm{N}$ has to be a failure of the assumptions.

 

[Chestermiller]

I'm going to try to make my point once more, assuming I have not been doing that well.

Let's pretend it the rod is in there touching both $A$ and $B$, we don't care how it got there, and we are not yet applying any load to the end.

When we start to apply the load in question to the end, the normal force at $B$ is going to decrease in magnitude, and the normal force at $A$ is going to increase. So if its calculated that $N_B = 327 \rm{N}$ after the load is applied (using pure statics), it has then necessarily decreased from some larger value it previously had at loads between zero and $F$. What value did it have before we applied the load? The only way we can specify that initial value from which it decreased is to specify how much the rod segment $AB$ was initially compressed to get it into the slot (given the properties of the rod). Given a final load of $F$ ( and a rigid bar), the normal force at $B$ must depend on the value it had before the load was applied. The idea that it inexplicably ends at $327 \rm{N}$ whether it was put in into the slot under $0.001 \rm{N}$ of compression or $1000 \rm{N}$ has to be a failure of the assumptions.

You are saying that AB was preloaded when it was put into place, and the amount of preload was unspecified. If we specify the amount of preload, then is it possible to determine the load at C without any force? and/or the load at C and the load where the guy's hand is located? I don't know. Please see if you can specify an initial case, not the same as the case in the actual problem.

 

[erobz]

You are saying that AB was preloaded when it was put into place, and the amount of preload was unspecified.

Yes if both points $A$ and $B$ are in contact after the load was applied , then segment $AB$ starts in a state of compression before any load was applied. If there is still $327~ \rm{N}$ of contact force after the load at the end of the bar is applied which works to decrease the normal force at $B$ ,then it certainly the contact force at $B$ was necessarily larger than $327 \rm{N}$ before the external load was applied. How much larger is an arbitrary function of just how much it was compressed to get it in there, but how much each contact force is altered by the external load would remain invariant.

If we specify the amount of preload, then is it possible to determine the load at C without any force? and/or the load at C and the load where the guy's hand is located?

I don't know about this.

I don't know. Please see if you can specify an initial case, not the same as the case in the actual problem.

It doesn't seem like that will be a trivial task.

 

[Chestermiller]

Yes if both points $A$ and $B$ are in contact after the load was applied , then segment $AB$ starts in a state of compression before any load was applied. If there is still $327~ \rm{N}$ of contact force after the load at the end of the bar is applied which works to decrease the normal force at $B$ ,then it certainly the contact force at $B$ was necessarily larger than $327 \rm{N}$ before the external load was applied. How much larger is an arbitrary function of just how much it was compressed to get it in there, but how much each contact force is altered by the external load would remain invariant.

I don't know about this.

It doesn't seem like that will be a trivial task.

Why can't there be zero contact loads on A, B, and C to start with?

 

[erobz]

Can it be in that position without any contact loads? I would say minimally it needs contact loads at $C$ and $B$ to be in that position.

 

[Chestermiller]

Can it be in that position without any contact loads? I would say minimally it needs contact loads at $C$ and $B$ to be in that position.

Why? Does it not fit geometrically, or are you considering the weight of the object?

 

[erobz]

Why? Does it not fit geometrically, or are you considering the weight of the object?

If it was in that position without any points of contact then the problem would be as I suggested in post #14. You can't have it both ways, there is either clearance in that position or there isn't.

 

[erobz]

Furthermore, lets say there is no clearance; $A, B$,and $C$ are all making contact with the force magnitude of beating fairy wings. When the force is applied, the lever would tend to rotate counterclockwise, pushing the rod into $A$, and away from $B$, and somehow according to the results of this problem we are to believe the rod is being driven into both A and B through this action. That the normal force at $B$ grows to $327 \rm{N}$ from zero ( in the limit). Someone better call up Rod Serling, I have a new episode for the Twilight Zone.

 

[Chestermiller]

Furthermore, lets say there is no clearance; $A, B$,and $C$ are all making contact with the force magnitude of beating fairy wings. When the force is applied, the lever would tend to rotate counterclockwise, pushing the rod into $A$, and away from $B$, and somehow according to the results of this problem we are to believe the rod is being driven into both A and B through this action. That the normal force at $B$ grows to $327 \rm{N}$ from zero ( in the limit). Someone better call up Rod Serling, I have a new episode for the Twilight Zone.

So are you saying that the final answer calculated by the OP is incorrect, non-unique, or what (irrespective of how the object got in that position)?

 

[erobz]

So are you saying that the final answer calculated by the OP is incorrect, non-unique, or what (irrespective of how the object got in that position)?

Non unique. The segment $AB$ was initially compressed (in pure statics that's already handwavy - all members are to be idealized as rigid ). In this problem the bar properties and the amount of compression are whatever they need to be, such that the Normals at $A$ and $B$ end up at their respective values. But if I changed the material of the bar for instance (and nothing else) I could make the values different (Imagine a wooden bar or a steel bar undergoing the necessary compression to fit into the slot).

In the end I would say its underspecified enough that it isn't incorrect. Maybe I'm just an a$$ for ranting about it.

 

[Chestermiller]

Non unique. The segment $AB$ was initially compressed (in pure statics that's already handwavy - all members are to be idealized as rigid ). In this problem the bar properties and the amount of compression are whatever they need to be, such that the Normals at $A$ and $B$ end up at their respective values. But if I changed the material of the bar for instance (and nothing else) I could make the values different (Imagine a wooden bar or a steel bar undergoing the necessary compression to fit into the slot).

In the end I would say its underspecified enough that it isn't incorrect. Maybe I'm just an a$$ for ranting about it.

You are not an ass, and I totally respect your abilities and judgment.

On this problem, however, I'm afraid we are going to have to agree to disagree. It seems to me that this problem is statically determinate, assuming that structure is stiff enough to resist substantial deformations. The rigid-body force and moment balances are linear in the reaction forces, and therefore must give a unique solution corresponding to the applied loading.

 

[Chestermiller]

@erobz On another topic, have you checked out my post # 52 in the thread on a can full of viscous Newtonian fluid rolling down a ramp?

 

[erobz]

@erobz On another topic, have you checked out my post # 52 in the thread on a can full of viscous Newtonian fluid rolling down a ramp?

I haven't given it much time yet, Its definitely over my level of training. When I do get around to trying to figure it out I'm sure I'll learn from it!