Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Karl R. Stromberg's book: "An Introduction to Classical Real Analysis". ... ...
I am focused on Chapter 3: Limits and Continuity ... ...
I need help in order to fully understand an aspect of Example 3.34 (c) on page 102 ... ... Examples 3.34 (plus some relevant definitions ...) reads as follows:
View attachment 9122
In Example 3.34 (c) above from Stromberg we read the following:
" ... ... Let $$\mathscr{I}$$ be the collection of all open intervals $$I$$ such that $$I \subset U$$ for some $$U$$ in $$\mathscr{U}$$. Check that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... "
My question is as follows:
How would we go about (rigorously) checking that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... indeed how would we rigorously demonstrate that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... ?
------------------------------------------------------------------------------------------------------------------------------
***EDIT***
My thoughts ... after reflecting ...$$\mathscr{U}$$ is an open cover (family of open subsets) of $$[a, b]$$ ... ...
Each set $$U \subset \mathscr{U} $$ is a countable set of pairwise disjoint open intervals ... ... (Theorem 3.18)
Therefore if $$\mathscr{I}$$ equals the collection of all open intervals $$I$$ such that $$I \subset U$$ ...
... then $$ \mathscr{I} $$ is a family of open intervals such that $$[a, b] \subset \bigcup \mathscr{I}$$ ...
Now apply Heine-Borel Theorem ...Is that correct?---------------------------------------------------------------------------------------------------------------------------------
Hope someone can help ...
Peter
========================================================================The above text from Stromberg mentions the Heine_Borel Theorem ... so I am proving the text of the (statement of ...) the theorem ... ... as follows:
View attachment 9123
"My thoughts ... ... " above include a reference to Theorem 3.18 ... the text of the statement of Theorem 3.18 is as follows:
View attachment 9124
View attachment 9125
Hope that helps ...
Peter
I am focused on Chapter 3: Limits and Continuity ... ...
I need help in order to fully understand an aspect of Example 3.34 (c) on page 102 ... ... Examples 3.34 (plus some relevant definitions ...) reads as follows:
View attachment 9122
In Example 3.34 (c) above from Stromberg we read the following:
" ... ... Let $$\mathscr{I}$$ be the collection of all open intervals $$I$$ such that $$I \subset U$$ for some $$U$$ in $$\mathscr{U}$$. Check that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... "
My question is as follows:
How would we go about (rigorously) checking that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... indeed how would we rigorously demonstrate that $$\mathscr{I}$$ is a cover of $$[a,b]$$ ... ... ?
------------------------------------------------------------------------------------------------------------------------------
***EDIT***
My thoughts ... after reflecting ...$$\mathscr{U}$$ is an open cover (family of open subsets) of $$[a, b]$$ ... ...
Each set $$U \subset \mathscr{U} $$ is a countable set of pairwise disjoint open intervals ... ... (Theorem 3.18)
Therefore if $$\mathscr{I}$$ equals the collection of all open intervals $$I$$ such that $$I \subset U$$ ...
... then $$ \mathscr{I} $$ is a family of open intervals such that $$[a, b] \subset \bigcup \mathscr{I}$$ ...
Now apply Heine-Borel Theorem ...Is that correct?---------------------------------------------------------------------------------------------------------------------------------
Hope someone can help ...
Peter
========================================================================The above text from Stromberg mentions the Heine_Borel Theorem ... so I am proving the text of the (statement of ...) the theorem ... ... as follows:
View attachment 9123
"My thoughts ... ... " above include a reference to Theorem 3.18 ... the text of the statement of Theorem 3.18 is as follows:
View attachment 9124
View attachment 9125
Hope that helps ...
Peter
Attachments
-
 Stromberg - Example 3.34 (c) ... .png30.5 KB · Views: 142
Stromberg - Example 3.34 (c) ... .png30.5 KB · Views: 142 -
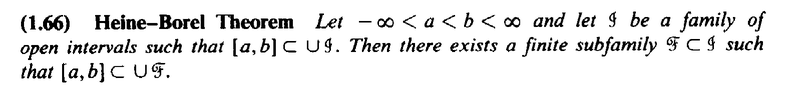 Stromberg - Statement of Heine-Borel Theorem 1.66 ... .png4.6 KB · Views: 125
Stromberg - Statement of Heine-Borel Theorem 1.66 ... .png4.6 KB · Views: 125 -
 Stromberg - 1 - Statement of Theorem 3.18 ... PART 1 ... .png6.3 KB · Views: 133
Stromberg - 1 - Statement of Theorem 3.18 ... PART 1 ... .png6.3 KB · Views: 133 -
 Stromberg - 2 - Statement of Theorem 3.18 ... PART 2 ... .png2.1 KB · Views: 152
Stromberg - 2 - Statement of Theorem 3.18 ... PART 2 ... .png2.1 KB · Views: 152
Last edited: