Comparetto type Air Cleaner/Filter: What causes its increased airflow?

[WilburWonka]

TL;DR

"DIY" Air filters have 2 widespread design types, Filter slapped on box-fan or 4 filters and a box fan joined to form a cube(the latter is known as Comparetto cube). The Comparetto gives a better airflow. I'd like to know if the venturi effect has anything to do with the superior airflow performance of this air cleaner type.

Typical box fan+air filter setups use axial consumer-grade fans designed for providing maximum air flow at low power consumption. These fans do not provide sufficient air flow at the high static pressure requirements typical of air filters. The air filters DIYers use are high Merv(e.g Merv 13) furnace filters, and those are meant to be paired with centrifugal fans, which deliver more air flow under high static pressure. As a result the filter-on-a-fan setup suffers from low air flow and potentially causes the fan to overheat. Here is an example of the filter-on-a-fan setup:



An improvement on this is the Comparetto cube:



The increase of the number of air filters leads to an increase in the air flow, and even despite the use of axial fans to move air through these filters, these air cleaners have airflow delivery comparable to that which the fan manufacturer specified. Fan manufacturers for these box fans typically state their fans air flow(CFM) for conditions in which no resistance was placed in the path of the fan. I take it to mean then that if an anemometer aided calculation for the air cleaner showed airflow in the same range as the box fans label air flow, then the resistance(static pressure drop) from the air filters was minimal from the Comparetto cube(at least while the filters are still new).

This can easily be attributed to the 4x increase in filter surface area, which means less CFM is passing through each filter so the resistance is less.

Have a look at this graph here relating filter face velocity to the resistance for an air filter( Specifically, these ones). I would hypothesize that the resistances from the air filters would add up something similar(not necessarily same) to resistance of resistors in a parallel circuit, so that the total resistance at a given air flow is lower than the resistance for each individual air filter. The total resistance-airflow graph of the filters would be flatter and therefore its intersection with the fan curve of the axial box-fans would be at a higher airflow.

(Here is a page explaining how that works: Skip to figure 6 for explanation. I'll also post the relevant image:)

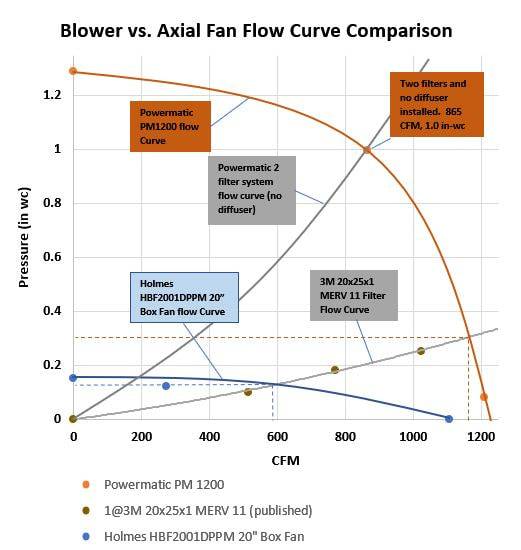
The point where the filters Resistance-Airflow curve(grey), intersects with a fans (static)Pressure-airflow curve(blue line is an axial fan, Orange line uses a centrifugal fan), gives the CFM the air cleaner will have(while the filter is still new at least).

Problem is: while all this is happening, the Comparetto cube doesn't just increase the filter mediums surface area, it seems to me, it is also increasing the cross sectional area the fluid(air) is passing through(4 times as large as the filter-on-box-fan setup). It seems to me that compared to the filter-on-box-fan setup, the air velocity is 4 times lower and the air pressure is four times higher at the Comparetto cubes filters' interfaces(Venturi effect). I'm not versed in fluid mechanics so I can't say if Bernoulli's equation applies like that in this 'system'. Is this so?

If they do, I'd think the increase in air pressure makes it easier for the filtered air to get through the air filters, so the air flow of the air cleaner is even more. In this case I'd like to know how to identify and maybe even calculate how much of that sweet CFM is a result of the Venturi effect and how much is a result of the decreased resistance due to more air filters.

 

[Lnewqban]

Welcome, WW!
I believe it is all about increased filtering area and reduced velocity of flow through it, and no Venturi effect in this arrangement.
Airflow coming from the sides must simultaneously turn and acelerate towards the low pressure area induced by the axial fan.

 

[256bits]

There is no Venturi effect.

and the air pressure is four times higher at the Comparetto cubes filters' interfaces(Venturi effect)

and that part is incorrect.
You can see that from the blue curve.
At maximum pressure that the fan can produce ( looks like 2.2 in WC ), there is no flow.
That would be maximum resistance to flow, ie cutoff.
As resistance decreases ( assume you unblock the fan and keep adding more filters ), fan pressure drops and cfm increases.

Neat way of cleaning air.

 

[russ_watters]

Problem is: while all this is happening, the Comparetto cube doesn't just increase the filter mediums surface area, it seems to me, it is also increasing the cross sectional area the fluid(air) is passing through(4 times as large as the filter-on-box-fan setup). It seems to me that compared to the filter-on-box-fan setup, the air velocity is 4 times lower and the air pressure is four times higher at the Comparetto cubes filters' interfaces(Venturi effect). I'm not versed in fluid mechanics so I can't say if Bernoulli's equation applies like that in this 'system'. Is this so?

This is a very common misapplication of the Venturi effect/Bernoulli's principle. The Bernoulli Equation/principle applies along a streamline; different parts of the airstream of one system/one Venturi tube. It does not apply (at least not the way you applied it) to comparing different systems to each other.

Also, it's a square function of velocity: a factor of 4 change in velocity is a factor of 16 change in velocity pressure. That's why your filter curves are curves -- though some do not exactly follow the square function (some are closer to linear).

Incidentally, a long while ago I did a thread where I ranted about the high cost/low value of consumer grade air purifiers. This <$100 "Comparetto cube" is way, way better than the $300 name-brand unit I bought my girlfriend at the time.

 

[Lnewqban]

Please, see:
https://www.thisoldhouse.com/green-home/22231148/diy-air-filter

 

[WilburWonka]

Thank you all for your responses. In summary, from what I have taken from the answers here, I take this to be the explanation:

The use of 4 filters increases the Filter face area(the box length and width of the filters- no stretching out the pleats) of the filter medium by 4, so the Filter face velocity(which is the Flow divided by the filter face area) is now a quarter for the same CFM air flow. The filter face velocity for the cube setup would therefore be a quarter of that for the 1-filter setup for the same cfm, and it would therefore have the corresponding lower resistance for that reduced face velocity(given by initial resistance vs filter face velocity chart).

As for the filter flow curve and fan flow curve intersection, which will determine the airflow from the air cleaner: the cube filters graph is basically like its been stretched 4x in relation to the y-axis. It intersects with the box-fan(axial) curve at a higher air flow rate, explaining why the cube type air cleaner has a better airflow performance(despite the low static pressure capabilities).

The Venturi effect doesn't apply here as per Russ's explanation.

The chart relation for resistance and face velocity is approximately Resistance = constant*(face velocity)^2, though this might differ between filter type and manufacturer.

Another question that came up: The air has to bend perpendicularly to the direction of the fans air flow in order to get through the filter. Does this result in an increase in static resistance? Say I used 4 filters joined together to form 1 big square filter, and then built a box with which had a place to put the fan infront of the combined filter, would this new setup have lesser resistance due to air not having to bend to get throw the filters. I'm mainly curious how much(if at all) does the resistance increase when air is having to bend perpendicular to its path to get to the exit(the filters, or the fan if the fan was in reverse direction).