Complete sets and complete spaces

[cromata]

-Definition of complete space: if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in converges in M. (and from this definition we can define Hilbert Space)
-Definition of Hilbert space:
A Hilbert space is a vector space

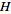with an inner product

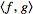such that the norm defined by

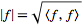
turns

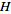into a complete metric space
-Definition of complete set: If V is inner product space and {e_k}_k∈ℕ is orthonormal set of vectors then we say that {e_k}_k∈ℕ is complete if for every u∈V u=∑<e_k,u>e_k

I have several questions:
-In infinite dimension inner vector spaces, infinite set of orthonormal vectors is not necessarily complete vector set? (is this true, and if it is, why?)

-Are complete sets and complete vector spaces connected in some way? Is every infinite set of orthonormal vectors in complete space (or more precisely in Hilbert space) complete set?

-What is the difference between complete set and basis?

 

[andrewkirk]

Definition of complete set: If V is inner product space and {e_k}_k∈ℕ is orthonormal set of vectors then we say that {e_k}_k∈ℕ is complete if for every u∈V u=∑<e_k,u>e_k

This contains a critical ambiguity - that you have not specified whether the sum is finite or infinite.
An orthonormal basis for a Hilbert space H is an orthonormal set of vectors whose span is dense in H.
An orthonormal Hamel basis for a Hilbert space H is an orthonormal set of vectors whose span is equal to H.

-In infinite dimension inner vector spaces, infinite set of orthonormal vectors is not necessarily complete vector set? (is this true, and if it is, why?)

Say $\{e_k\}_{k\in\mathbb N}$ is a basis. Then the infinite, orthonormal subset $\{e_{2k}\}_{k\in\mathbb N}$ of even-numbered elements of the set, is not complete (because if it were the original set would not be linearly independent), and hence not a basis.

-What is the difference between complete set and basis?

As I learned it, completeness of a set of vectors does not entail linear independence. If a complete set is not linearly independent, it is not a basis. But your definition above includes orthonormality, which entails linear independence, so your definition looks the same as that of either an orthonormal Hamel basis (if the sums must be finite) or an orthonormal basis (if they can be infinite).

 

[mathman]

These definitions are not restricted to Hilbert spaces. They apply to any vector space, where there is a defined norm.