Loro
- 79
- 0
Homework Statement
Hi, I need to calculate the following integral:
\int_{-\infty}^{+\infty}dx \frac{(\pi+\sqrt{x^2+m^2})^2(1+\cos x)}{(x^2-\pi^2)^2\sqrt{x^2+m^2}}
The Attempt at a Solution
I tried complexifying it:
\oint dz \frac{(\pi+\sqrt{z^2+m^2})^2(1+e^{iz})}{(z^2-\pi^2)^2\sqrt{z^2+m^2}}
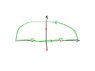
And having this over the following contour (sorry for the quality of the image):
https://www.dropbox.com/s/t7ioou1kjs3y7ej/paint.jpg?dl=0
The red dots are the poles at: \pm\pi and \pm im.
But is it a valid contour in this case, or should I pay extra attention to the branch cuts of the sqrt in the denominator? If so, how do I choose the contour properly?