Akibarika
- 8
- 0
Little help in compound pendulum
there is an equilateral triangle T with sides of length B. Suspend this triangle from a pivot through on of its corners, so that it is free to swing about this corner in the plane of the tringle.
I want to ask how to compute the density p(x,y) and the R whcih from the pivot point to the center of gravity of the triangle.
In fact I found the soluation, but I don't know it is right or not.
Could anyone check it with me?
p(x,y)=m/A
A=sqrt(3)/4 * B^2
therefore p(x,y)=(4*sqrt(3)*m)/(3*B^2)
about the R:
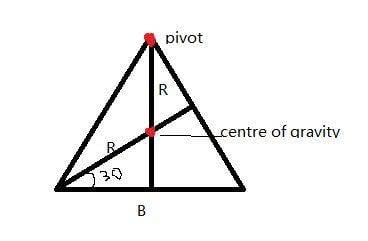
cos 30 = sqrt(3)/2
R = (B/2)*(2/sqrt(3)) = (sqrt(3)*B)/3
did I make any mistake??
Thanks a lot
Homework Statement
there is an equilateral triangle T with sides of length B. Suspend this triangle from a pivot through on of its corners, so that it is free to swing about this corner in the plane of the tringle.
I want to ask how to compute the density p(x,y) and the R whcih from the pivot point to the center of gravity of the triangle.
In fact I found the soluation, but I don't know it is right or not.
Could anyone check it with me?
Homework Equations
p(x,y)=m/A
The Attempt at a Solution
A=sqrt(3)/4 * B^2
therefore p(x,y)=(4*sqrt(3)*m)/(3*B^2)
about the R:
cos 30 = sqrt(3)/2
R = (B/2)*(2/sqrt(3)) = (sqrt(3)*B)/3
did I make any mistake??
Thanks a lot
Last edited: