dylanreynolds1
- 2
- 2
Hello all, first post.
I have come here to get second opinions on the program I have written to compute the Einstein Tensor (the Riemann Tensor and Ricci Tensor). I enjoy looking for solutions to the Einstein Field Equations, however computing them by hand is not realistic. I decided to write a program, but I am by no means a programmer.
The program takes in a particular form of the metric, and outputs the Ricci Tensor. Since I am mostly interested in vacuum solutions at the moment, this is all I need. I have copied in the Python code below, however I am sure there is a better way to display it.
Any ideas about how to make the program better, or how to make a better post on this forum are greatly appreciated, however my main goal is to hear form people who know more about GR than me.
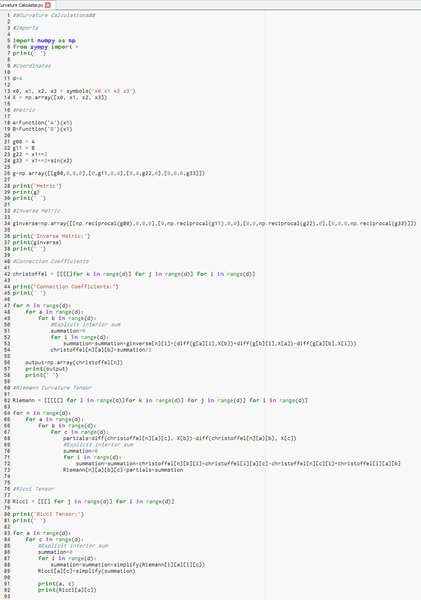
This code has helped me derive the Schwarzschild solution, so it must be at least somewhat accurate. However there may be some small detail that I have missed.
Any help would be much appreciated.
I have come here to get second opinions on the program I have written to compute the Einstein Tensor (the Riemann Tensor and Ricci Tensor). I enjoy looking for solutions to the Einstein Field Equations, however computing them by hand is not realistic. I decided to write a program, but I am by no means a programmer.
The program takes in a particular form of the metric, and outputs the Ricci Tensor. Since I am mostly interested in vacuum solutions at the moment, this is all I need. I have copied in the Python code below, however I am sure there is a better way to display it.
Any ideas about how to make the program better, or how to make a better post on this forum are greatly appreciated, however my main goal is to hear form people who know more about GR than me.
This code has helped me derive the Schwarzschild solution, so it must be at least somewhat accurate. However there may be some small detail that I have missed.
Any help would be much appreciated.
Last edited: