- #1
erkant
- 20
- 0
I even don't know if this is the appropriate place to post this questions, while as long as I know this place is considered for research topics and more advanced topics in physics. The point is that I need to write a MATLAB code for specific question, but first of all I need to solve it, and show the step by step solution of it, and then code it. Because I am not that good in physics, I though maybe someone where can give me a step by step solution, so I can code it later.
Here is the question:
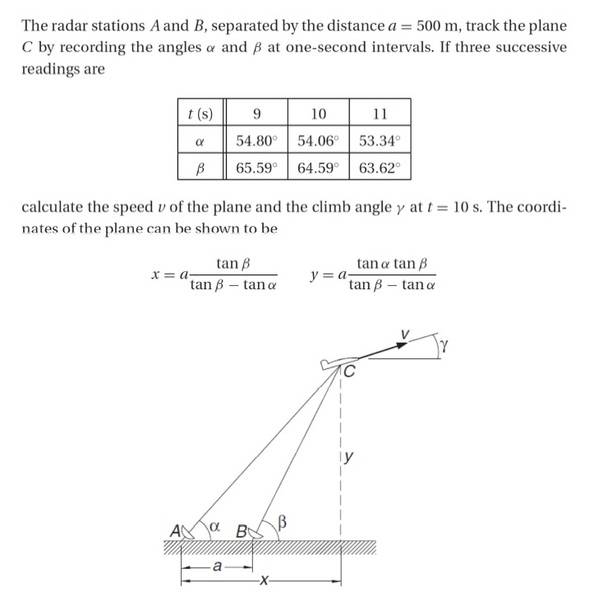
Here is the question:
Attachments
Last edited by a moderator:
