Conceptual question about FBDs and KDs

[mbigras]

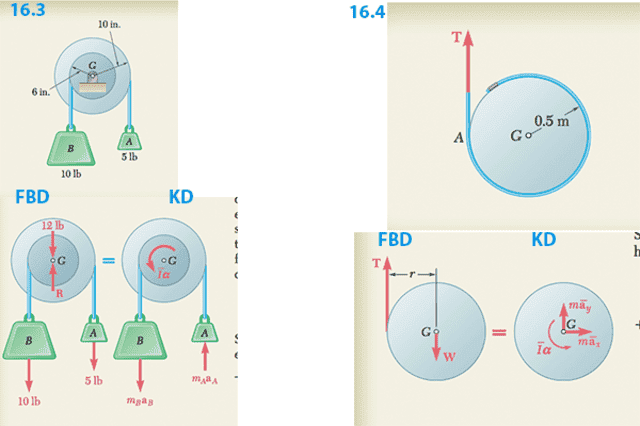
I'm looking at example 16.3 and 16.4 in Beer and Johnson vector mechanics dynamics. It seems that you can draw the forces in your FBD as "effective forces" on your KD (kinetic diagram). I'm confused about how I should choose to draw the effective forces at the centroid G or to draw them where they are acting. In example 16.3 the forces are drawn where they are acting, but in 16.4 they are drawn at the centroid.

One hypothesis that I have is: if the body is in fixed axis rotation then draw the effective forces where they are acting but if the body is in general plane motion then draw the effective forces at the centroid.

Also I'm very interested to hear some helpful ways that you imagine going between drawing forces on a FBD and drawing the effective forces on the KD. I'm taking engineering classes as a physics major and this is my first exposure to effective forces and I'm having trouble understanding where the \bar{I}\vec{\alpha} and the different effective force terms come from.

 

[AlephZero]

I don't have the book, so I don't know how prescriptive it is about the "right" way to draw the diagrams.

The diagrams are just a (very useful) tool, to help you write the equations of motion, $F = ma$ and $T = I\dot\omega$. The FBD shows what goes on left hand side of the equations. the KD shows what goes on the right hand side.

On the FBD, the simplest thing to do is draw all the forces at the points where they act.
On the KD, I would start by drawing the vectors that describe the acclerations of the system. For a rigid body, a simple way to do that is to show the translation and rotation of the center of mass. Then, multiply the accelerations by the corresponding mass or inertia values.

The diagrams 16.3 and 16.4 both follow those "rules".

If 16.3 the FBD is for the complete system, so it doesn't show the tensions in the two strings which are internal forces. But to write equations of motion, you might want to draw FBDs for the three parts A B and C separately, and then you do need to show the tensions. (But if you are going to solve the problem using energy methods, you won't need to do that.)

 

[mbigras]

thanks for the response. I was reading through the book section 16.7 on page 1048 addresses my confusion. AlephZero also said it. The key difference between 16.3 and 16.4 is that 16.3 is a "system of rigid bodies" with one member in fixed axis rotation which explains why we only see the couple and no effective force, and two members in translation which explains why we only see the effective forces but no couples. 16.4 is a "single rigid body" >>>>that is in general plane motion aka rotation and translation? Is this right?<<<<<< which explains why we see both an effective force and the couple.

 

[AlephZero]

It isn't that 16.3 has several rigid bodies and 16.4 has only one.

The difference is that in 16.3 there is a constraint on how body C can move (the axle that supports it). Its center of mass can not move, so its displacement, velocity, and acceleration are all zero. But it can rotate about the axle, so it can have an non-zero angular acceleration.

If you were being pedantic, the masses A and B could have angular accelerations as well, except there are no forces that would make them rotate, so drawing an angular acceleration and then writing an equation that says it is 0 is rather pointless. Similarly, it is obvious that A and B will only move vertically, not horizontally.

In 16.4 the motion of the disk is not constrained in any way, so its center of mass can both translate in any direction, and also rotate.