- #1
GCUEasilyDistracted
- 3
- 7
I've started reading the Principia and have been trying to follow along with the examples. Unfortunately, I got stuck almost immediately. This example is from 'Axioms, or laws of motion', Law III, Corollary II. It is based on the following picture (everything in red is my addition):
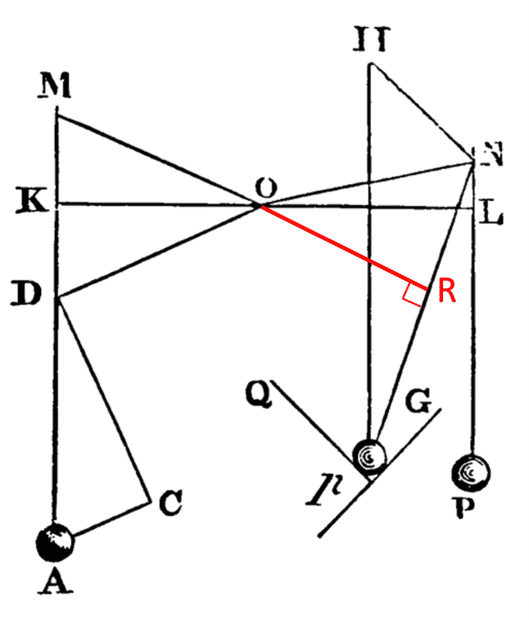
The text states "As if the unequal radii ##OM## and ##ON## drawn from the centre ##O## of any wheel, should sustain the weights ##A## and ##P## by the cords ##MA## and ##NP##; and the forces of those weights to move the wheel were required...If the weight ##p##, equal to the weight ##P##, is partly suspended by the cord ##Np##, partly sustained by the oblique plane ##pG##; draw ##pH##, ##NH##, the former perpendicular to the horizon, the latter to the plane ##pG##; and if the force of the weight ##p## tending downwards is represented by the line ##pH##, it may be resolved into the forces ##pN##, ##HN##." It later says "therefore if the weight ##p## is to the weight ##A## in a ratio compounded of the reciprocal ratio of the least distances of the cords ##PN##, ##AM##, from the centre of the wheel, and of the direct ratio of ##pH## to ##pN##, the weights will have the same effect towards moving the wheel, and will therefore sustain each other." I was trying to make sense of this and derive the result.
The least distances of the cords ##PN## and ##AM## from the center ##O## should refer to the lengths of the lines ##OL## and ##OK## respectively if I'm correct. So, the "reciprocal ratio" of these ought to be ##\frac{\overline{OK}}{\overline{OL}}##. The "direct ratio" of ##pH## to ##pN## should just be ##\frac{\overline{pH}}{\overline{pN}}##. So the way I interpret the second statement I quoted is that the forces due to weights ##A## and ##p## will be balanced on the wheel, resulting in zero torque, if
$$\frac{m_p}{m_A} = \frac{\overline{OK}}{\overline{OL}}\frac{\overline{pH}}{\overline{pN}}$$ $$(Eq. 1)$$
Here I'm also assuming that the weight ##P## is not included under consideration.
While trying to derive this relationship, I attempted to calculate the magnitudes of the torques due to each weight.
$$\tau_A = \overline{OK}m_Ag$$
$$\tau_p = \overline{OR}T_{pN}$$
##T_{pN}## is the magnitude of tension in the cord ##pN##.
Note that ##T_{pN} = m_pg\frac{\overline{pN}}{\overline{pH}}##. Therefore,
$$\tau_p = \overline{OR}m_pg\frac{\overline{pN}}{\overline{pH}}$$
Setting ##\tau_A = \tau_p## gives
$$\overline{OK}m_Ag = \overline{OR}m_pg\frac{\overline{pN}}{\overline{pH}}$$
$$\overline{OK}m_A = \overline{OR}m_p\frac{\overline{pN}}{\overline{pH}}$$
$$\frac{m_p}{m_A} = \frac{\overline{OK}}{\overline{OR}}\frac{\overline{pH}}{\overline{pN}}$$ $$(Eq. 2)$$
Equation 2 is almost the same as Equation 1, it's just that ##\overline{OL}## is replaced by ##\overline{OR}##. If the statement "the least distances of the cords ##PN##, ##AM##, from the centre of the wheel" were replaced with "the least distances of the cords ##pN##, ##AM##, from the centre of the wheel" (note the lowercase ##p##), then it would be identical since the least distance of ##pN## from ##O## is in fact ##\overline{OR}##.
Where am I going wrong? I really appreciate any help with this.
The text states "As if the unequal radii ##OM## and ##ON## drawn from the centre ##O## of any wheel, should sustain the weights ##A## and ##P## by the cords ##MA## and ##NP##; and the forces of those weights to move the wheel were required...If the weight ##p##, equal to the weight ##P##, is partly suspended by the cord ##Np##, partly sustained by the oblique plane ##pG##; draw ##pH##, ##NH##, the former perpendicular to the horizon, the latter to the plane ##pG##; and if the force of the weight ##p## tending downwards is represented by the line ##pH##, it may be resolved into the forces ##pN##, ##HN##." It later says "therefore if the weight ##p## is to the weight ##A## in a ratio compounded of the reciprocal ratio of the least distances of the cords ##PN##, ##AM##, from the centre of the wheel, and of the direct ratio of ##pH## to ##pN##, the weights will have the same effect towards moving the wheel, and will therefore sustain each other." I was trying to make sense of this and derive the result.
The least distances of the cords ##PN## and ##AM## from the center ##O## should refer to the lengths of the lines ##OL## and ##OK## respectively if I'm correct. So, the "reciprocal ratio" of these ought to be ##\frac{\overline{OK}}{\overline{OL}}##. The "direct ratio" of ##pH## to ##pN## should just be ##\frac{\overline{pH}}{\overline{pN}}##. So the way I interpret the second statement I quoted is that the forces due to weights ##A## and ##p## will be balanced on the wheel, resulting in zero torque, if
$$\frac{m_p}{m_A} = \frac{\overline{OK}}{\overline{OL}}\frac{\overline{pH}}{\overline{pN}}$$ $$(Eq. 1)$$
Here I'm also assuming that the weight ##P## is not included under consideration.
While trying to derive this relationship, I attempted to calculate the magnitudes of the torques due to each weight.
$$\tau_A = \overline{OK}m_Ag$$
$$\tau_p = \overline{OR}T_{pN}$$
##T_{pN}## is the magnitude of tension in the cord ##pN##.
Note that ##T_{pN} = m_pg\frac{\overline{pN}}{\overline{pH}}##. Therefore,
$$\tau_p = \overline{OR}m_pg\frac{\overline{pN}}{\overline{pH}}$$
Setting ##\tau_A = \tau_p## gives
$$\overline{OK}m_Ag = \overline{OR}m_pg\frac{\overline{pN}}{\overline{pH}}$$
$$\overline{OK}m_A = \overline{OR}m_p\frac{\overline{pN}}{\overline{pH}}$$
$$\frac{m_p}{m_A} = \frac{\overline{OK}}{\overline{OR}}\frac{\overline{pH}}{\overline{pN}}$$ $$(Eq. 2)$$
Equation 2 is almost the same as Equation 1, it's just that ##\overline{OL}## is replaced by ##\overline{OR}##. If the statement "the least distances of the cords ##PN##, ##AM##, from the centre of the wheel" were replaced with "the least distances of the cords ##pN##, ##AM##, from the centre of the wheel" (note the lowercase ##p##), then it would be identical since the least distance of ##pN## from ##O## is in fact ##\overline{OR}##.
Where am I going wrong? I really appreciate any help with this.