Conformability elastic material compressed on a wavy surface

[SolMech]

Hey there,

I'm struggling in finding the useful equations to determine some conformability parameters for a finite elastic material (EPDM) compressed on a rigid slightly wavy surface. I would like to optimize the thickness of the elastic material in terms of indentation depth and thus contact area and pressure. To describe the situation I've added the following picture.

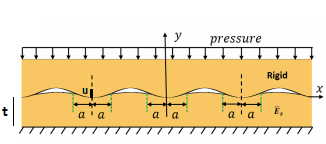
I would like to determine indentation depth u in terms of thickness t, pressure P and elastic modulus E. Could you assist me in finding the solution.

 

[Chestermiller]

My inclination would be to solve this using finite element, particularly if the depth of the undulations is significant (compared to the thickness of the elastic material). You can use a "unit cell" consisting of half the wave laterally. I can't think of a simple "strength of materials" approximation that would work on this.