- #1
peanutaxis
- 24
- 3
In the first diagram below, there is a horizontal board and it is attached to a vertical board via a pivot, P, but is also hooked via a nail (red), and the vertical board is resting on the ground.
If I am pulling on the horizontal board with force Fp, and the whole setup doesn't move, then the forces on the vertical board are Fp, Ff, and F?. Since it is not moving Fp + Ff + F? = 0, and also the torques on the vertical board - due to Ff and F? - about P are equal and opposite (I should have made Ff look smaller).
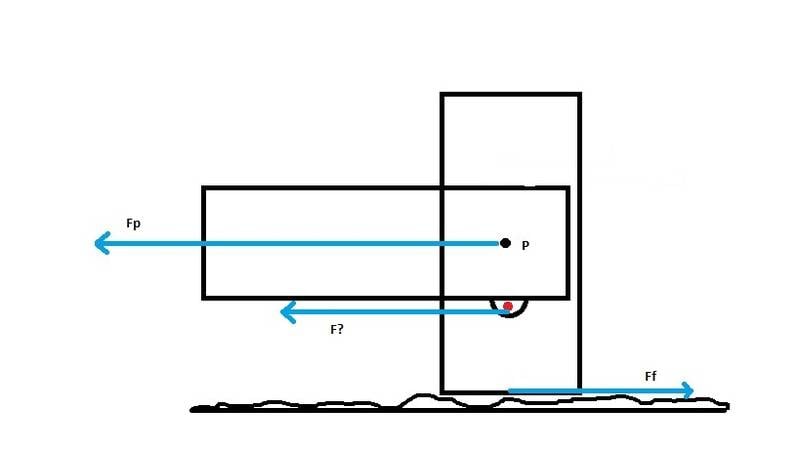
In the second diagram (also nothing is moving) the nail and hook are now moved to the bottom. Fp is still the same, and Ff is also the same since the weight of the system and the frictioned ground are the same. Even F? is the same since the vertical board is still not rotating so the torques due to Ff and F? will still add to zero. But now F? is in the same direction as Fp, and so the horizontal forces aren't going to sum to zero anymore.
Intuitively, it shouldn't make any difference where you place the nail and hook. Wherever you place them, they will create the same torque about P, but all of a sudden it doesn't make sense in the second diagram.
What the heck is going on?:huh::huh:
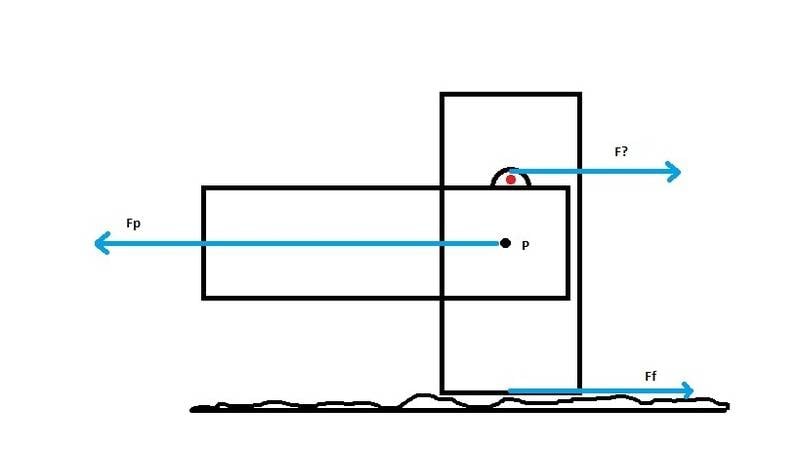
If I am pulling on the horizontal board with force Fp, and the whole setup doesn't move, then the forces on the vertical board are Fp, Ff, and F?. Since it is not moving Fp + Ff + F? = 0, and also the torques on the vertical board - due to Ff and F? - about P are equal and opposite (I should have made Ff look smaller).
In the second diagram (also nothing is moving) the nail and hook are now moved to the bottom. Fp is still the same, and Ff is also the same since the weight of the system and the frictioned ground are the same. Even F? is the same since the vertical board is still not rotating so the torques due to Ff and F? will still add to zero. But now F? is in the same direction as Fp, and so the horizontal forces aren't going to sum to zero anymore.
Intuitively, it shouldn't make any difference where you place the nail and hook. Wherever you place them, they will create the same torque about P, but all of a sudden it doesn't make sense in the second diagram.
What the heck is going on?:huh::huh: