Confusion about tidal locking and rotational kinetic energy

[arestes]

Hello!
I was reading two things:

1) tidal locking (as explained in the Wikipedia article:https://en.wikipedia.org/wiki/Tidal_locking

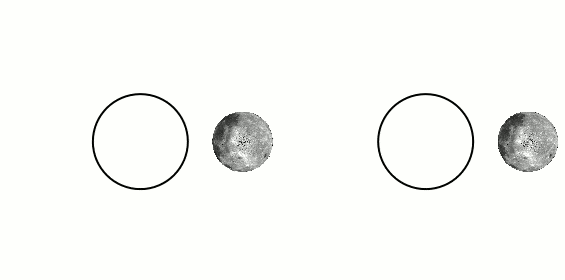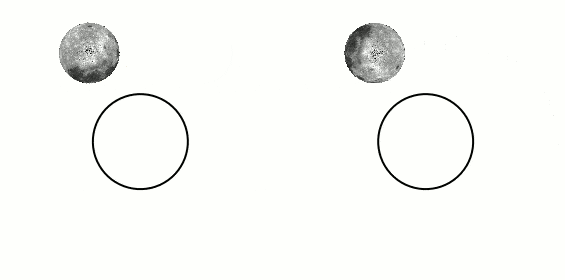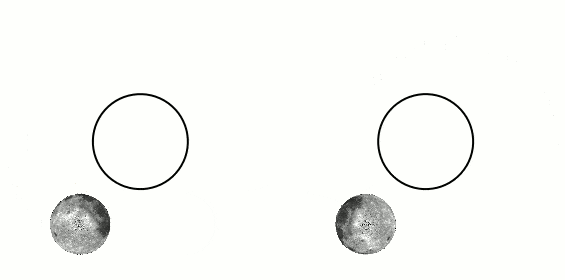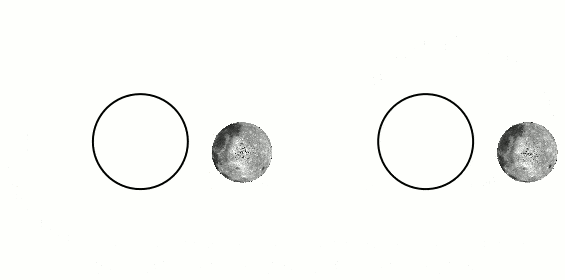
where it is stated that, because of internal friction caused by the body of water being attracted to the moon and deforming, the kinetic energy of the system Earth-Moon diminishes as time passes, giving rise to tidal locking. This explains why the left figure above has less kinetic energy and is the final state of the system after some time. This makes sense.2) Chabay and Sherwood's not-so-popular but (I believe) well thought-out book "Matter and Interactions". Here, they split Kinetic energy into Rotational and Translational. They put up two examples in which a bar (with two small spheres) is rotated about a point, by virtue of a light rod. See figures 11.81 and 11.82. Figure 11.81 shows the bar rotating in such a way that its orientation remains fixed (vertical) while rotating around the central point. The other figure shows the bar rotating around the bar's own center and while this very center rotates around the original center. The first one (11.81) is said to have less angular momentum than 11.82 because 11.81 has no "intrinsic" rotation about its own axis. I assume that this argument also shows that the first (bar with unchanging orientation) has less kinetic energy.

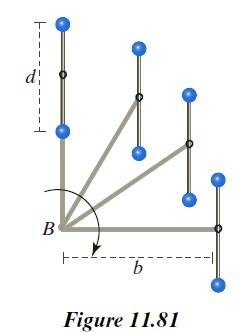
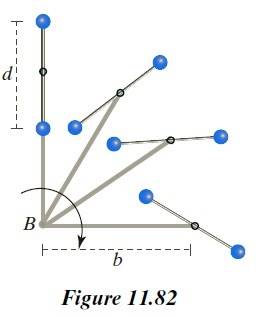
But... this contradicts the wikipedia article that requires that the rigid body rotating lose energy and starts showing the same face to the center (the Earth), which means its orientation keeps changing.

What am I getting wrong?

Any help would be appreciated.

 

[Dale]

What am I getting wrong?

You need to consider both the angular momentum and the energy of both the Earth and the moon.

Stopping the rotation of the moon would make it have less energy, but also less angular momentum. That reduced angular momentum would need to go into the earth, which would require a substantially larger increase of KE.

Also, even if that configuration had less energy there would be no way to get to it.

 

[arestes]

I see. So, if I understand correctly:

Chabay- Sherwood is right and the rotating bar does have more energy/angular momentum.
However, this is not the case for the Earth-Moon system as I need to consider both bodies, and it's better for the system to stay locked to avoid giving more angular momentum to the Earth because the Earth would contribute disproportionally to the total kinetic energy if given more angular momentum.(by looking at the formulas of kinetic energy as a function of angular speed squared as opposed to angular momentum which depends on angular speed only). Am I right?

One more question, please: I'm trying to see how being locked minimizes the energy of the Earth-Moon system while conserving the angular momentum. It should be the case that in this locked state, energy remains constant, right? Can this be proven easily? I also read that there are "resonances" for this locking mechanism such as in the case of Mercury and the Sun (3:2). This makes me believe this is not very simple. Any pointers as to how this is proved?
Thanks

 

[DrStupid]

Stopping the rotation of the moon would make it have less energy, but also less angular momentum. That reduced angular momentum would need to go into the earth, which would require a substantially larger increase of KE.

A part of the angular momentum goes into the orbital angular momentum, increasing the distance and therefore the potential energy of the system. This will also reduce the orbital kinetic energy of the moon but that doesn't outweight the increase of the potential energy (due to the virial theorem).