Confusion over the calculation of the angular momentum of a rigid body

[timetraveller123]

Homework Statement

this has been bugging me for a while now the angular momentum about any point p is given as
$\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + L_{cm}\\$
now if the body precessing around z axis and spinning about its own axis then angular velocity of body in lab frame is
$\vec \omega = \Omega \hat z + {\omega '} \hat s$
then if you are going to calculate angular momentum in cm frame then in cm frame you don't observe the $\Omega \hat z$ term so you isn't the angular momentum just
$\vec {L_{cm}} = (I_{xx} {\omega '}_x , I_{yy} {\omega '}_y , I_{zz} {\omega '}_z)$
I have seen this come up in many texts and I am starting to get confused over it. thanks for any help

Homework Equations

The Attempt at a Solution

 

[TSny]

Homework Statement

this has been bugging me for a while now the angular momentum about any point p is given as
$\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + L_{cm}$

It is important to understand the interpretation of the term $\vec L_{cm}$ in this relation. If you want to interpret this as the angular momentum of the system relative to the cm frame, then you have to be careful. Is the relation valid if the cm frame rotates relative to the lab frame?

now if the body precessing around z axis and spinning about its own axis then angular velocity of body in lab frame is
$\vec \omega = \Omega \hat z + {\omega '} \hat s$

OK

then if you are going to calculate angular momentum in cm frame then in cm frame you don't observe the $\Omega \hat z$

Is this true if the cm frame does not rotate relative to the lab frame?

Here's an example to consider.

You have a thin horizontal rod that rotates about the z-axis as shown with angular speed $\Omega$ and also spins with angular speed $\omega '$ about its length. For simplicity, take the special case where $\omega '$ is zero, so the rod just rotates about the z axis. The red axes denote the cm frame of reference.

Try applying the relation $\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + \vec {L_{cm}}$ and see if you get what you would expect for the angular momentum of the system. Consider two cases:
(1) The cm axes rotate with the rod so that the y ' axis is always along the rod
(2) the cm axes do not rotate relative to the lab frame, so the y ' axis remains parallel to the y axis as the rod rotates about the z axis.

 

[timetraveller123]

Is this true if the cm frame does not rotate relative to the lab frame?

this is not true if the cm does not rotate relative to lab frame but I assumed it does

then for the example

1)
L relative to the origin of lab frame is R$\times$ M $\Omega$ R + $\frac{M}{12} (2R)^2 \Omega$
where the last term is because in the cm frame the rod appears to rotate about the cm orgin

2) I am assuming the cm is now fixed in the origin of the lab (I don't see any other way the rod can rotate about z axis)
so the angular momentum is just
L relative to the origin of lab frame is 0$\times$ M $\Omega$ R + $\frac{M}{12} (2R)^2 \Omega$

is this correct and thanks for your effort to make such a detailed reply

 

[TSny]

1)
L relative to the origin of lab frame is R$\times$ M $\Omega$ R + $\frac{M}{12} (2R)^2 \Omega$
where the last term is because in the cm frame the rod appears to rotate about the cm orgin

In case (1) the cm-frame axes rotate with the rod. So in this case there is no rotation of the rod relative to the cm-frame axes. Therefore, this is the case that would correspond to your statement in the first post where you said,

then if you are going to calculate angular momentum in cm frame then in cm frame you don't observe the $\Omega \hat z$ term

Then for this example, the term $L_{cm}$ in the the relation $\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + \vec {L_{cm}}$ would be zero. So, this would lead to the result $\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}}$, which is incorrect.

2) I am assuming the cm is now fixed in the origin of the lab (I don't see any other way the rod can rotate about z axis)
so the angular momentum is just
L relative to the origin of lab frame is 0$\times$ M $\Omega$ R + $\frac{M}{12} (2R)^2 \Omega$

In case (2) the rod still rotates about one end as in the figure. The figure is still applicable. But as the center of mass revolves around the z-axis of the lab frame, the red cm-frame axes remain parallel to the lab frame axes. So, in this case, the rod does rotate relative to the red cm-frame axes with angular velocity $\Omega \hat z$. So, now you do observe $\Omega \hat z$ in the cm frame. Therefore $L_{cm}$ is not zero. You should now find that the relation $\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + \vec {L_{cm}}$ gives the correct result for the angular momentum of the rod relative to the lab frame origin.

 

[timetraveller123]

wait I am sorry but I am confused than ever now
in case 1)
my reasoning was that in the centre of mass of frame one end appears to move back and the other end appears to move forward relative to the cm due to their different distances from the axis of rotation thus giving rise to apparent rotation in the cm frame but now that you say there is no rotation in cm frame then in the angular momentum relation there shouldn't be any $L_{cm}$ thus shouldn't $L_P$ be just $M \Omega R$ where does the $\frac{M}{12} (2R)^2 \Omega$ term come from I know this is just an application of parallel axis theorem but how to do it without the parallel axis theorem
for case 2) I completely cannot visualize how the cm can not be in the origin and still the cm axis axes parallel to lab axes please help me with that

I think it would help if you could help me with the basics
for a point mass it is just
$L_P = M \Omega R^2$
there is no $L_{cm}$ due its neglible size
for collection of particles it is just
$\sum m_i \omega_i r_i$
for rigid bodies it can be described as movement of cm plus movement about cm thus
it becomes
$L_P = MVR + I \omega$
if there is no rotation about cm(like you said in case 1) then the second term is zero then why doesn't the angular momentum reduce to just $L_{cm}$(which you said is incorrect)

I am sorry if I am getting what you are saying and thanks once again

 

[TSny]

Let’s go back to your first post where you stated that $\Omega \hat z$ is not observed in the cm frame. Can you describe what you mean by the cm frame and can you explain why $\Omega \hat z$ is not observed in this frame?

 

[timetraveller123]

okay sir If I may take detour I was reading a text where it mentioned

"
Another important point to note is that the angular velocity is the same for both laboratory frame and the rotating frame because the angle made by a line on the body wrt a reference line is the same in both the frames. Contrast this with the linear velocity; the velocities in the two frames differ by the relative velocity between the two frames.
"
I am not really understanding why this is true it would help a lot because this would show that $\Omega \hat z$ is observed in both frames

now answering your question I related it analogously to linear motion say cm is moving at 5m/s wrt lab and a point on the body is moving 7m/s wrt lab then the point is moving 2m/s wrt cm
but one possible answer I can think of as to why such analogy can't be applied to rotation is that even if something moving at constant angular velocity it is still accelerating thus the frame is not inertial and it ends up observing that it is the one that is moving ie in the cm frame the $\Omega \hat z$ is observed
is this hypothesis correct ?
thanks once again

 

[TSny]

We are considering the relation

$\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + \vec {L_{cm}} \,\,\,\,\,\,\,\, [1]$

This equation applies to any system of particles. $p$ is a fixed point in the "lab" frame. Our difficulty is with the last term $\vec {L_{cm}}$. If you review the derivation of equation [1], you will see that this term is

$\vec {L_{cm}} = \sum m_i \vec r_{i,cm} \times \vec v_{i,cm}$.

Here, $\vec r_{i,cm} = \vec r_{i,p} - \vec R_{cm,p}$ where $\vec r_{i,p}$ is the position of the $i$^th particle relative to the lab point $p$ and $\vec R_{cm,p}$ is the position of the cm relative to the lab point $p$.

What is the meaning of $\vec v_{i,cm}$? This is where confusion can occur.

A review of the derivation of equation [1] shows that $$\vec v_{i,cm} \equiv \frac{d \vec r_{i,cm}}{dt} = \frac{d \vec r_{i,p}}{dt} - \frac{d \vec R_{cm,p}}{dt}$$ where all time derivatives represent rates of change relative to the lab frame. Is it possible to interpret $\vec v_{i,cm}$ also as the rate of change of $\vec r_{i,cm}$ relative to the cm frame?

To answer this, we can invoke an important fact about switching frames of reference. Suppose we have an arbitrary time dependent vector $\vec A(t)$ that we observe from two different frames of reference. We can let one of the frames be our lab frame and let the other frame be a frame moving with the cm. It is not hard to show that as long as the two frames have no rotation relative to one another, then the rate of change of $\vec A(t)$ is the same in both frames. (Neglecting relativistic effects, of course). That is, $$\frac{\vec A(t)}{dt}|_{lab} = \frac{\vec A(t)}{dt}|_{cm}$$
So, as long we take the cm frame to be nonrotating relative to the lab frame, we can interpret $\vec v_{i,cm}$ in the expression for $\vec {L_{cm}}$ in equation [1] as the velocity of the $i$^th particle relative to the cm frame.

If the cm frame is rotating relative to the lab frame then it is not generally true that $\large \frac{\vec A(t)}{dt}|_{lab} = \frac{\vec A(t)}{dt}|_{cm}$. You can find details here http://www.whoi.edu/cms/files/12.800_Chapter_4_'06_25333.pdf. The punch line is equation 4.1.6.

So, all of this was meant to show that when considering the term $\vec {L_{cm}}$ in equation [1] as angular momentum relative to a cm frame, it is important that the cm frame not be rotating relative to the lab frame.

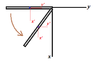
Going back to the example of the rotating rod of post #2, a top view would look like

The red frame is the cm frame and it does not rotate relative to the lab frame. In the red frame, the rod rotates with the same angular velocity $\Omega$ as in the lab frame.

 

[TSny]

As a quick exercise, consider a solid disk of mass M and radius R rolling without slipping as shown. You can use $\vec {L_p} = \vec {R_{cm,p}} \times \vec {P_{cm}} + \vec {L_{cm}}$ to find the angular momentum of the disk about the point P in terms of V_cm, M and R.

 

[timetraveller123]

sir sorry for the very late reply i was traveling and had net issues sorry
in post 8) i understand what you are saying i am familiar with the transformation but i am afraid you did not answer my question of a definitive way to calculate L
but i think your next post may help
post 9)
i am familiar with these kind of problems it is simply just
$L = MVR + \frac{1}{2} M R^2 \omega$
the kind that trip me up are when i need to calculate it in the frame of cm like this

there in the question in the para the cm was chosen as origin and in calculating the L about cm why do they include the $\Omega \hat z$term because that is the motion of the centre of mass i understand that that term would be used when calculating in lab frame but why in ball frame

 

[TSny]

in calculating the L about cm why do they include the $\Omega \hat z$term because that is the motion of the centre of mass i understand that that term would be used when calculating in lab frame but why in ball frame

Equation (8.164) is the "spin" part of the angular momentum of the ball relative to the lab frame, not relative to "the frame rotating with angular velocity $\Omega \hat z$" . That is, (8.164) represents the term $\vec L_{cm}$ in the equation $\vec L_p = \vec R_{cm,p} \times \vec P_{cm} + \vec L_{cm}$. (The first term on the right is the "orbital" part of the angular momentum due to motion of the cm about the fixed point p in the lab. This part is not included in equation (8.164).)

As mentioned before, $\vec L_{cm}$ represents the net angular momentum of all the particles of the ball relative to the origin of a coordinate system whose origin coincides with the center of the ball, but the axes of the coordinate system do not rotate relative to the lab. $\Omega \hat z$ contributes to the total angular velocity of the ball about its center from the point of view of this frame (as given in (8.163)). Since this frame does not rotate relative to the lab frame, (8.163) also gives the "spin" angular velocity of the ball relative to the lab frame.

 

[timetraveller123]

ooh now i see what you mean is it something like this
while the question mentions around cm at an instant it doesn't mention it calculates in the cm frame but instead a fixed frame whose origin coincides with the cm at the particular instant
but i don't think you would call the $\Omega \hat z$ orbital i think it is also spin angular momentum because at that instant the cm at (0,0) is this correct

 

[TSny]

ooh now i see what you mean is it something like this
while the question mentions around cm at an instant it doesn't mention it calculates in the cm frame but instead a fixed frame whose origin coincides with the cm at the particular instant

Yes.

but i don't think you would call the $\Omega \hat z$ orbital i think it is also spin angular momentum because at that instant the cm at (0,0) is this correct

Yes. I didn't mean to imply that $\Omega \hat z$ is "orbital". It is part of the spin angular velocity as given in (8.163). Let me try to clarify what I wrote as

Equation (8.164) is the "spin" part of the angular momentum of the ball relative to the lab frame, not relative to "the frame rotating with angular velocity $\Omega \hat z$" . That is, (8.164) represents the term $\vec L_{cm}$ in the equation $\vec L_p = \vec R_{cm,p} \times \vec P_{cm} + \vec L_{cm}$. (The first term on the right is the "orbital" part of the angular momentum due to motion of the cm about the fixed point p in the lab. This part is not included in equation (8.164).)

When I referred to the "first term on the right", I was referring to the first term on the right of the equation $\vec L_p = \vec R_{cm,p} \times \vec P_{cm} + \vec L_{cm}$. That is, I was referring to the term $\vec R_{cm,p} \times \vec P_{cm}$ as the orbital angular momentum part. I wasn't referring to the first term on the right of equation (8.163): $\Omega \hat z$.

By choosing the origin in the lab frame to be instantaneously coincident with the center of mass of the ball, the orbital part of the angular momentum is zero since $\vec R_{cm,p} = 0$.
Thus, $\vec L_p = \vec R_{cm,p} \times \vec P_{cm} + \vec L_{cm}$ reduces to $\vec L_p = \vec L_{cm} = I \vec \omega$.

I shouldn't have said that (8.164) doesn't include the orbital part. Since the orbital part is zero (due to the choice of origin), you can consider (8.164) as including it!

 

[timetraveller123]

ok thanks it is starting to make sense now but looking back now i think there is something wrong with our reasoning

you asked to interpret $L_{cm}$ as measured by a stationary frame centered at the cm at that instant but that does not make sense for the following reason
then in that frame letting that be s'

if s' were to be be stationary it would measure the left end moving $\Omega r$ and the the right end moving with $\Omega (r + D)$ this corresponds to no sort of rotation about z' axis but if we let z' move with the cm this problem is cleared because z' is itself moving with $\Omega (r + 1/2 D)$ then the relative velocity of left end and right end is $\omega ( -1/2 D)$ and$\Omega (1/2 D)$ respectively. which does correspond to rotation of $\Omega$ about the z' axis then we can go ahead and use the angular momentum neglecting the orbital part as you said
so what i am saying is that after all this while the term $L_{cm}$ was meant to be calculated in cm frame and not in stationary frame
is this reasoning valid

 

[TSny]

The question appears to be, "What coordinate frame should be used to calculate $\vec L_{\rm cm}$ at some instant of time?" It turns out that you can use either of the following two frames:

(1) A frame that is fixed in the lab and has origin that coincides with the cm at the instant of time of interest. Call this frame $S$.

(2) A frame that moves with the cm, has origin at the cm, and doesn't rotate relative to the lab. Call this frame $S'$.

You can prove that you will always get the same result for $\vec L_{\rm cm}$ in the two frames. At first this may appear to be impossible since, as you noted, an individual particle of the system will generally have different velocities in the two frames. If $\vec v_i '$ is the velocity of the $i_{\rm th}$ particle in $S'$, then the velocity of the particle in $S$ is $\vec v_i = \vec v_i ' + \vec v_{\rm cm}$. Here, $\vec v_{\rm cm}$ is the velocity of the cm relative to frame $S$.

In frame $S$,

$\vec L_{\rm cm} = \sum \left( m_i \vec r_i \times \vec v_i \right) = \sum \left[ m_i \vec r_i \times \left(\vec v_i ' + \vec v_{\rm cm} \right) \right] = \sum \left( m_i \vec r_i \times \vec v_i ' \right) + \sum \left( m_i \vec r_i \times \vec v_{\rm cm} \right)$.

Argue that the last term on the far right is zero. So, $\vec L_{\rm cm} = \vec L_{\rm cm}'$.

 

[timetraveller123]

wait why would that the last term be zero i seen cases where
$\sum (m_i r'_i \times v_{cm}) = 0$
due to definition of cm but why is that term zero

 

[BvU]

Don't forget the vector sign. $\vec v_{\rm cm}$ in $S$ does not depend on $i$ so you can interchange summation and vector multiplication. What does the summation give you ?

 

[TSny]

wait why would that the last term be zero i seen cases where
$\sum (m_i r'_i \times v_{cm}) = 0$
due to definition of cm but why is that term zero

$\vec r_i '= \vec r_i$.

 

[timetraveller123]

$\vec r_i '= \vec r_i$.

oh you $r'_i = r_i$ i forgot that now it makes sense

here is one more example
there are two identical coins one coin is rolling without slipping over the other fixed coin find the angular momentum of rolling coin with respect to the fixed coins centre

so orbital angular velocity $\Omega$ = spin angular velocity $\omega$
thus
$\vec L = M 2\vec r \times ( \Omega \times (2 \vec r) + I (\Omega \hat z + \omega \hat z) \\ \vec L = 4Mr^2 \Omega \hat z + I (2\Omega \hat z )$

 

[TSny]

here is one more example
there are two identical coins one coin is rolling without slipping over the other fixed coin find the angular momentum of rolling coin with respect to the fixed coins centre

so orbital angular velocity $\Omega$ = spin angular velocity $\omega$
thus
$\vec L = M 2\vec r \times ( \Omega \times (2 \vec r) + I (\Omega \hat z + \omega \hat z) \\ \vec L = 4Mr^2 \Omega \hat z + I (2\Omega \hat z )$

Yes, that looks good. The meaning of $\omega$ here is similar to the meaning of $\omega '$ defined in the basketball problem in post #10.

 

[timetraveller123]

ok thanks for the help until now i will continue looking for interesting problems and ask you here if something puzzles but thanks for the help