Eggue
- 13
- 2
- Homework Statement
- A solid cylinder with mass M and radius R, rotating with angular speed about an axis through its center, is set on a horizontal surface for which the kinetic friction coefficient is (a) Draw a free-body diagram for the cylinder on the surface. Think carefully about the direction of the kinetic friction force on the cylinder. Calculate the accelerations of the center of mass and of rotation about the center of mass. (b) The cylinder is initially slipping completely, so initially but Rolling without slipping sets in when Calculate the distance the cylinder rolls before slipping stops
- Relevant Equations
- Kinematic equations
I'm not sure as to why my working is incorrect. When the sign on a_x is positive, i get t = \frac{R\omega_0}{3\mu_kg} which would give the correct value for distance if plugged into the kinematic equation. However, I'm not sure why a_x would be positive though since the friction force is pointing in the direction of -x
Working:
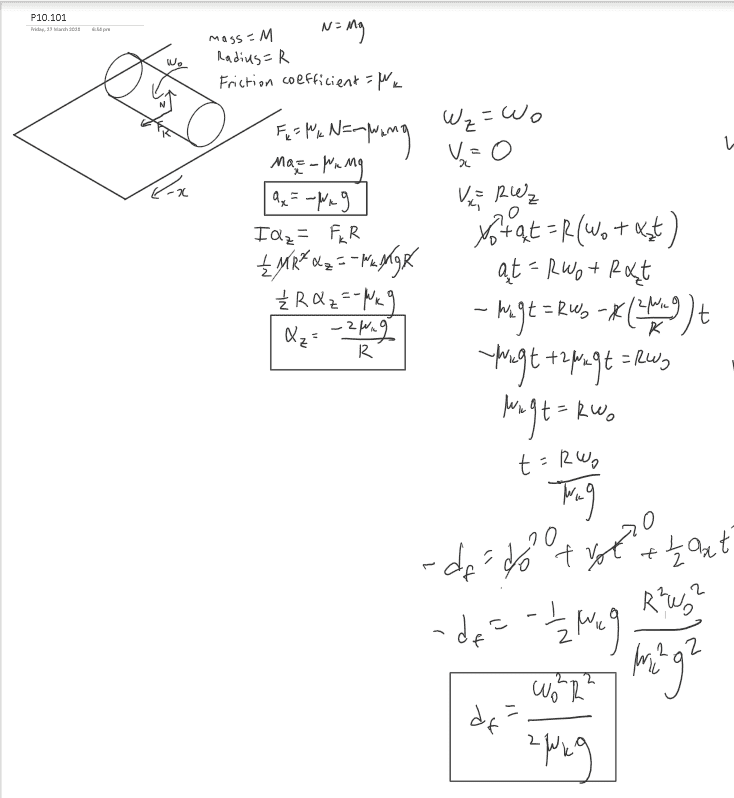
Working: