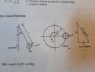
SUMMARY
The discussion centers on the conical pendulum's height issue, specifically when the height (h) exceeds the string length (L). It is established that the period of the conical pendulum, given by the formula T=2π√(h/g), must be less than that of a planar pendulum, which is approximately 3.5 seconds for a 3m string. The critical condition for the conical pendulum's existence is Lω² ≥ g; otherwise, the radius becomes zero or imaginary. The conversation highlights the importance of correctly specified values for real solutions in pendulum problems.
PREREQUISITES
- Understanding of conical pendulum dynamics
- Familiarity with angular frequency and harmonic motion
- Knowledge of gravitational acceleration (g)
- Basic grasp of pendulum motion equations
NEXT STEPS
- Study the derivation of the conical pendulum period formula T=2π√(h/g)
- Explore the implications of the condition Lω² ≥ g on pendulum motion
- Investigate the relationship between angular frequency and pendulum amplitude
- Learn about the effects of varying string lengths and heights on pendulum behavior
USEFUL FOR
Physics students, educators, and anyone interested in the mechanics of pendulums and circular motion dynamics.