Conservation of energy minimum speed

[firezap]

Homework Statement

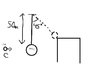
Gus is at end of rope. He needs to reach roof. His friend fires cannon ball horizontally hitting Gus and get stuck in belt. Find minimum speed of cannon ball for Gus to reach roof. 50m is rope. 99kg is Gus. 1kg is ball. 45° angle in diagram

Homework Equations

conservation of energy
Et1 = Et2
1/2mv^2 = mgh
momentum
p = mv

The Attempt at a Solution

1/2(1)v^2 = 99(9.8)(50xsin45°)
1/2v^2 = 34301.75
v = 260 m/s
is this right?

 

[firezap]

conservation of energy:
1/2 (m+M) V² = (m+M)gh
V² = 2gh
conservation of momentum:
mv = (m+M)V
v = (m+M) sqrt(2gh) / m
is this correct?

 

[kris2fer]

Yes.

 

[Doc Al]

conservation of energy:
1/2 (m+M) V² = (m+M)gh
V² = 2gh
conservation of momentum:
mv = (m+M)V
v = (m+M) sqrt(2gh) / m
is this correct?

Looks good. The collision of cannonball and person is treated as an inelastic collision.

 

[Nickie]

I would say that your solution is correct based on the given information and equations. However, I would also suggest considering the conservation of momentum in addition to the conservation of energy. Since the cannon ball gets stuck in the belt, there is a transfer of momentum from the ball to Gus. Therefore, the equation for conservation of momentum (p = mv) should also be taken into account when solving for the minimum speed of the cannon ball. This will provide a more complete and accurate solution to the problem.