- #1
aaaa202
- 1,169
- 2
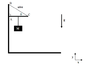
Consider the equilibrium situation on the picture attached.
The wire supports a rod attached to an axle in the wall and the mass is suspended at about half the length from the point where the where the wire is attached (the exact position is unimportant for my point).
We neglect friction from the wall. My question is: Is this equilibrium possible? Because in order for the center of mass of the rod not to fall the wires vertical force component must equal mg. But then that would mean, that it exerted a bigger torque than the mass forcing the rod to rotate anticlockwise. What would happen in this situation and is it possible to model without friction?
The wire supports a rod attached to an axle in the wall and the mass is suspended at about half the length from the point where the where the wire is attached (the exact position is unimportant for my point).
We neglect friction from the wall. My question is: Is this equilibrium possible? Because in order for the center of mass of the rod not to fall the wires vertical force component must equal mg. But then that would mean, that it exerted a bigger torque than the mass forcing the rod to rotate anticlockwise. What would happen in this situation and is it possible to model without friction?