Construct a Moore Circuit for Binary String '01' Detection: Step-by-Step Guide"

[DenDanne]

Summary:: I have a problem getting the circuit of the problem to a Moore-solution.

"Construct a Moore Machine and show it in a circuit, that outputs '1' whenever the sequence '01' is encountered in any input binary string (using D-flipflops)".

First of, I have written the Moore Machine.

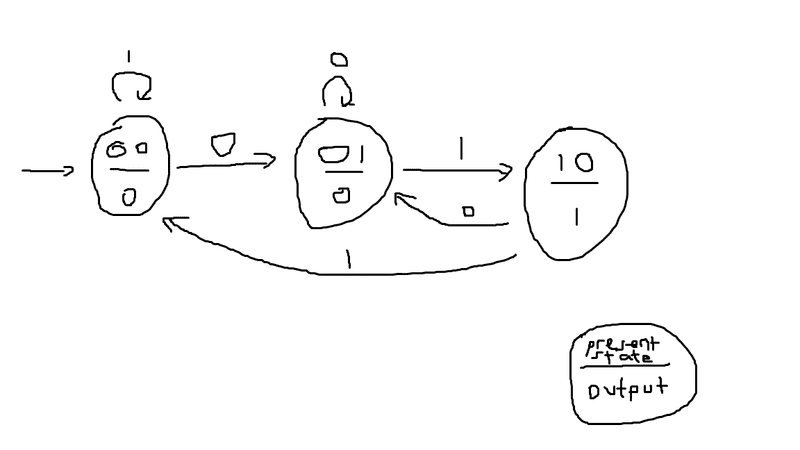
I don't think this is where the problem is, as it is quite straight forward in that step.

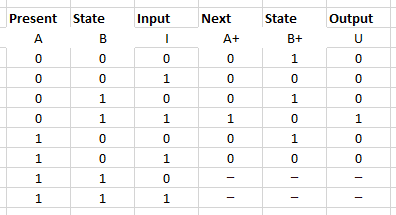
From this Moore Machine, I do a truth table.

And then I use Karnough-diagrams to find equations for A+, B+ and U.

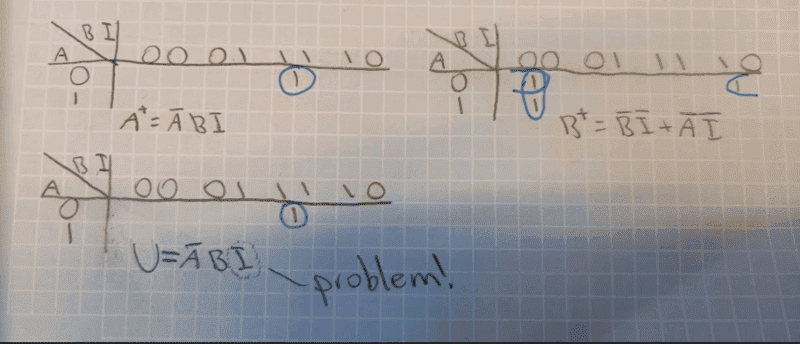
Here is where I get some troubles.
Because by definition of Moore machines. The output shall only be a result of the present state and some output combinatorial logic. NOT the the input. (that is mealy). But as you can see, I get an I in the output formula. So using this method I get an output dependent on the input, which is not allowed!

What have I thought wrong about?

 

[berkeman]

Welcome to PF.

The next state does depend on the input and the current state, as you have shown. The output only depends on the state, so get rid of the I term in that equation -- it is not used.

 

[DenDanne]

Welcome to PF.

The next state does depend on the input and the current state, as you have shown. The output only depends on the state, so get rid of the I term in that equation -- it is not used.

Thanks!
But if I Karnough without input I, then I get U=A'B. And the problem with this is that there are two times when 01 is the state. Or should I use Karnough on A+ and B+ (next states), that would solve the problem since A+ is only 1 once. But I have never used Karnough on "next states" before.

 

[berkeman]

When you are in state 01, the output is 1, and it is 0 otherwise. You have 2 FFs in the circuit, so the combinatorial circuit to generate the output takes the outputs of the two FFs as inputs.

If they are DFFs, the input D terms come from the two K-maps that you have above for the next state.

 

[DenDanne]

When you are in state 01, the output is 1, and it is 0 otherwise. You have 2 FFs in the circuit, so the combinatorial circuit to generate the output takes the outputs of the two FFs as inputs.

If they are DFFs, the input D terms come from the two K-maps that you have above for the next state.

But according the the State Diagram. The output is 0 when I am in state 01? Only in 10 is the output 1. Hence, I'm thinking that U=AB' is correct for U?

 

[berkeman]

Oh, sorry, I misread your table. The output in your table should depend on the current state, like this example:

http://www.ee.surrey.ac.uk/Projects/CAL/seq-switching/state_diagrams_and_state_tables.htm