Constructing Bending Moment Diagram for Member 1-5 Using Stiffness Matrix Method

[MMCS]

This problem has a lot of calculations from the beginning so i have skipped to the part i am stuck with and tried to include relevant information, apologies if i have missed anything. Assume all working is correct as i was given the answers.

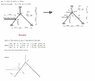
After carrying out the stiffness matrix method I am trying to construct a bending moment diagram using member equilibrium, see attached.

The specific problem is member 1-5

working

member 1-4

bending moment at 1 (given) 123.33Kn
vertical force 57.44Kn
length 2.5

therefore

123.33 - 57.44Kn*2.5 = -20.27 (correct)

Member 4 -5
-20.67 + 160KN(moment from pre-eliminated beam) = 139.63Kn (correct)

however i can not get the moment of -123.98 at point 5

attempt member 4-5
vertical force relative to beam = 80 (sin(36.87)
moment = 139.63Kn
139.63Kn - 80 sin(36.87)*2.5 = 19.629 (incorrect)

 

[paisiello2]

It's difficult to follow what you doing here but is there not a shear force at point 4 in addition to the 80?

 

[MMCS]

It's difficult to follow what you doing here but is there not a shear force at point 4 in addition to the 80?

Yes I appreciate it is fairly difficult to follow. Essentially I have got the bending moments on one side using stiffness matrix method and the used these values and member equilibrium for the rest of the beam. There is a shear force yes, I have tried to account for that, that's why I have used 80sin(36.87) as this would give me the vertical component of the force (vertical relative to the member)

 

[paisiello2]

The shear force is the internal shear in addition to the 80 external force.

 

[MMCS]

The shear force is the internal shear in addition to the 80 external force.

Would that have to be included in the bending moment diagram? If so, how is the force calculated? And would it be used in the same way as a vertical force e.g F x distance

 

[paisiello2]

1) Yes.

2) Same way you got the bending moment at point 4.

3) Yes.

 

[MMCS]

1) Yes.

2) Same way you got the bending moment at point 4.

3) Yes.

I got the moment by using (UDL x L) x L/2 ?

 

[paisiello2]

But you added another term to it as well.

 

[MMCS]

But you added another term to it as well.

Yes I added the moment from point one. For point 5 this is the method I have tried. I don't follow what you are suggesting?

 

[paisiello2]

OK, we are trying to get the moment at point 5, correct? So you need to take the moment at point 4 plus the shear at point 4 multiplied by L = 2.92m.

The shear at point 4 is 80kN*sin(37.9°) plus the shear from member 4-1.

 

[MMCS]

OK, we are trying to get the moment at point 5, correct? So you need to take the moment at point 4 plus the shear at point 4 multiplied by L = 2.92m.

The shear at point 4 is 80kN*sin(37.9°) plus the shear from member 4-1.

Attempt

139.63-((80sin(37.9))+57.44)*25 = -126.83

This is pretty close to -123.98 but still off,

Have i made an error?

 

[paisiello2]

You probably made a rounding error.