Constructive and destructive interference

[PainterGuy]

Hi,

It said that constructive interference has taken place between two waves if the combined amplitude for two waves at a certain time is more than their individual amplitudes. Likewise, in case of destructive interference, the combined amplitude is less than the individual amplitudes of either waves.

Moreover, when total or complete constructive interference takes places between two waves, the combined amplitude is sum of individual amplitudes and the waves are totally in phase. For complete or total destructive interference, the combined amplitude is zero and the waves are totally out of phase with each other.

I hope that what I said above is correct.

Question 1:
I'm sure any two waves would always interfere with each other; sometimes constructively and other times destructively. But would they always happen to interfere totally destructively or constructively?

Question 2:
This one is related to Question 1.

I'm also trying to find a way to see at what time total destructive and constructive interference takes place. In Case 1 only frequencies are different and for Case 2 in addition to frequencies being different wave #1 is also 30 degrees phase shifted.

How do I proceed?

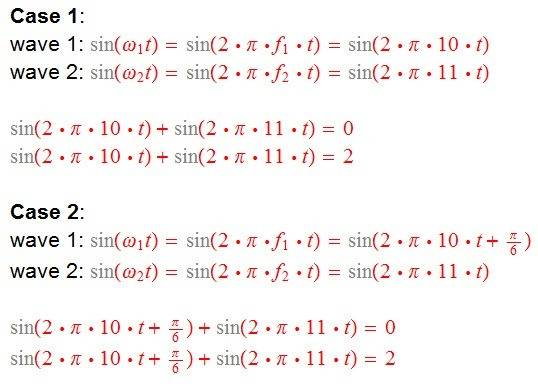
Thank you for the help.

 

[Charles Link]

The simplest case to look at is two point sources that radiate sinusoidal disturbances=waves, radially outward each with spherical symmetry. These sources are often studied for the pattern they make in a given plane. This is basically what the two slit interference pattern is all about. The intensity of the signal is proportional to the square of the sinusoidal amplitude. Let me try to find a "link" for you. This is perhaps the simplest case that has regions of constructive and destructive interference. The mathematics for the interference pattern is most easily described in the far-field, i.e. far away from the two point sources. See http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/coursenotes/modules/guide14.pdf
Normally, for the sinusoidal disturbance, they use the function $E(t)=E_o \cos(\omega t+\phi)$. You can also work with $\sin(\omega t)$instead of $\cos(\omega t)$, but the customary convention is to use $\cos(\omega t)$.

 

[sophiecentaur]

Summary: Little confused about constructive and destructive interference definitions, and also trying to mathematically find when total constructive and destructive interference takes places.

But would they always happen to interfere totally destructively or constructively?

A fixed interference pattern will only occur when the two waves are either of the same frequency (coherent enough). The position / time of coincident addition or subtraction will, in general, be constantly changing and can't be identified as an interference pattern.
I am not sure what your calculations are supposed to be showing. The equation of a Wave is of the form
A = A₀ cos (ωt- kx)
To calculate an interference pattern, you add two such waves together and use trig identities to get the answer for a particular location and time. The wiki page tells you all you need to know, I think. It's very common just to show the positions of maxes and mins but the overall variation can be found and shows details of the pattern.

 

[mfb]

Several posts have been moved to a new thread.