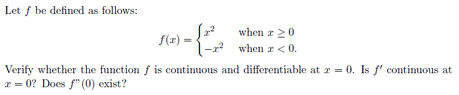Continuous and differentiability

Click For Summary
SUMMARY

The discussion centers on the continuity and differentiability of a function defined piecewise, specifically at the point \(x=0\). The function's first derivative is established as \(f'(x) = 2x\) for \(x \geq 0\) and \(f'(x) = -2x\) for \(x < 0\). The user seeks guidance on demonstrating the existence of the second derivative \(f''(0)\). It is confirmed that \(f\) is differentiable at \(0\) with \(f'(0) = 0\).

PREREQUISITES
  • Understanding of piecewise functions
  • Knowledge of basic calculus, specifically differentiation
  • Familiarity with the concept of limits
  • Ability to apply the definition of differentiability
NEXT STEPS
  • Study the definition and properties of piecewise differentiable functions
  • Learn how to compute higher-order derivatives
  • Explore the concept of continuity and differentiability at points of non-smoothness
  • Investigate the implications of differentiability on the existence of higher derivatives
USEFUL FOR

Students and educators in calculus, mathematicians focusing on analysis, and anyone interested in understanding the nuances of differentiability in piecewise functions.

Joe20
Messages
53
Reaction score
1
Hello,

I have attached the question and the steps worked out. I am not sure if my steps are correctly. Need advise on that.
Next, I am not sure how to show f''(0) exist or not. Thanks in advance!
 

Attachments

  • Webp.net-resizeimage.jpg
    Webp.net-resizeimage.jpg
    30.6 KB · Views: 113
  • 2..png
    2..png
    7.2 KB · Views: 137
Physics news on Phys.org
You have shown that $f$ is differentiable at $0$ and that $f'(0) = 0$. For $x\ne0$ you can use the usual rules for differentiation, to see that $f'(x) = 2x$ if $x>0$ and $f'(x) = -2x$ if $x<0$. Therefore \[f'(x) = \begin{cases}2x&\text{when }x\geqslant0,\\-2x&\text{when }x<0.\end{cases}\] Now you have to decide whether that function is differentiable at $x=0$.
 

Similar threads

MHB Piecewise function: differentiable but not continuously differentiable
  • · Replies 21 ·
Replies
21
Views
2K
MHB Understanding Differentiability and Continuity in Complex Analysis
  • · Replies 2 ·
Replies
2
Views
2K
MHB Compactness and Continuity in R^n .... .... D&K Theorem 1.8.8 .... ....
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Proving a function f is continuous given A U B = X
  • · Replies 5 ·
Replies
5
Views
3K
MHB Complex and Real Differentiability .... Remmert, Section 2, Ch. 1 .... ....
  • · Replies 1 ·
Replies
1
Views
1K
MHB Relationship Between Total Derivatives and Directional Derivatives .... ....
  • · Replies 3 ·
Replies
3
Views
2K
MHB Continuity of f^+ .... Browder Corollary 3.13
  • · Replies 4 ·
Replies
4
Views
2K
MHB F is partially differentiable in (0,0) but not total differentiable
  • · Replies 11 ·
Replies
11
Views
2K
MHB Lipschitz Continuity .... and Continuity in R^n ....
  • · Replies 3 ·
Replies
3
Views
2K
MHB Proper and Continuous Mappings in R^n .... ....
  • · Replies 2 ·
Replies
2
Views
1K