Converting Area to Volume: A Spherical Coordinate Approach

[brioches]

Homework Statement

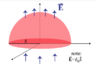
A hemispherical surface of radius b = 61 m is fixed in a uniform electric field of magnitude E0 = 3 V/m as shown in the figure. The x-axis points out of the screen.

Enter the general expression for an infinitesimal area element dA in spherical coordinates (r, θ, φ) using n as your outward-pointing normal vector. In these coordinates θ is the polar angle (from the z-axis) and φ is the azimuthal angle (from the x-axis in the x-y plane).

Homework Equations

φ(flux) = ∫ E dA

The Attempt at a Solution

I understand that we're supposed to be looking for a small piece of area, but I don't know what makes up that area. We had a triple integral last semester of ∫∫∫r²dr sin(θ)dθ dφ. Is that related? We used that to integrate the volume of a sphere. Is there a similar process one can use for area?

 

[PeroK]

I guess you can either look up the area element in spherical coordinates or work it out for yourself from first principles.

 

[haruspex]

∫∫∫r²dr sin(θ)dθ dφ. Is that related?

Very much so. Suppose you had an area element dA for a shell radius r within the sphere. How would you turn it into a volume element? Compare that with the integrand above.