Coriolis Force on a Wheel of radius r spinning at angular velocity

[kaamlot92]

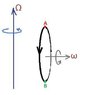
Imagine that we have a wheel spinning with the axis of rotation normal to the Earth's surface. For convenience, let's assume that the wheel is located somewhere in the north hemisphere.

According to the definition of the Coriolis force, every little particle dm of the wheel has a coriolis force in some direction. But if we integrate to get the coriolis force on the whole object, doesn't the integral go to 0 since we are in a circle?

Further, if we consider the torque on the wheel due to the coriolis force, we know that the torque is defined as: τ = r' x F.coriolis . where r' is the vector position of dm relatively to the CM of the wheel.

Since the coriolis force is zero, doesn't it mean that the torque is also zero?

(I know that the answer is no, but why? and where does the torque point...?)

 

[TSny]

Hello and welcome to PF!

It will be simpler to analyze if the wheel is located at the equator. Then the axis of rotation of the wheel is perpendicular to the axis of rotation of the earth. See attached figure. The axis of rotation of the Earth is represented by the blue vertical arrow and Ω is the rate of rotation of the earth. The wheel is rotating with angular velocity ω.

Consider the elements of mass marked A and B on the wheel. Note that relative to the Earth the velocity of A at this moment is essentially out of the page while B is moving into the page.

What is the direction of the coriolis force on A? On B?