- #1
kidsasd987
- 143
- 4
Hi, I am a little confused of derivation of Coulomb Gauage.
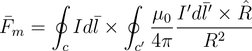 (2)
(2)
First, prime notation is adopted to describe the magnetic field density source current.
Non-prime notation is for position that we are specifically interested in (ex. the position magnetic force acts on).
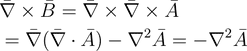 (23)
(23)
if equation (13) is true, then divergence of vector potential is 0.Hence,
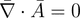 (13)
(13)
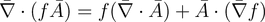 (14)we can use vector indentity (14) to express (13) in another form.
(14)we can use vector indentity (14) to express (13) in another form.
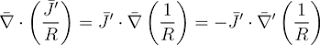 (15)
(15)
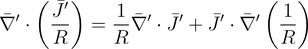 (16)
(16)
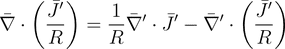 (17)
(17)
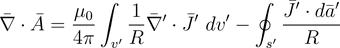 (18)
(18)
at this step, I am lost. We can break down divergence of vector potential into
two parts. I understand the first part is 0 because we assume that the field is static with respect to time,
but I wonder why the second flux integral part is 0.
(reference: http://ghebook.blogspot.ca/2011/06/energy-of-magnetic-field.html)
First, prime notation is adopted to describe the magnetic field density source current.
Non-prime notation is for position that we are specifically interested in (ex. the position magnetic force acts on).
if equation (13) is true, then divergence of vector potential is 0.Hence,
at this step, I am lost. We can break down divergence of vector potential into
two parts. I understand the first part is 0 because we assume that the field is static with respect to time,
but I wonder why the second flux integral part is 0.
(reference: http://ghebook.blogspot.ca/2011/06/energy-of-magnetic-field.html)
Last edited: