JasonHathaway
- 113
- 0
Hi everyone, this my first post in here.
Anyway, this is a solved problem, but I can't get the answer :S
* Series-Parallel combination (RT=R1+R2+R3...+Rn for series, 1/RT=1/R1+1/R2+1/R3...+1/Rn for parallel)
* WYE (TEE) - DELTA (PI) Transformations:
1- WYE (TEE) to DELTA (PI): Each resistor in the DELTA (PI) is equal to the sum of all possible products of WYE (TEE) resistors taken two at a time, divided by the opposite WYE (TEE) resistor.
2- DELTA (PI) to WYE (TEE): Each resistor in the WYE (TEE) is equal to the product of the resistors in two adjacent DELTA (PI) branches, divided by the sum of all three DELTA (PI) resistors.
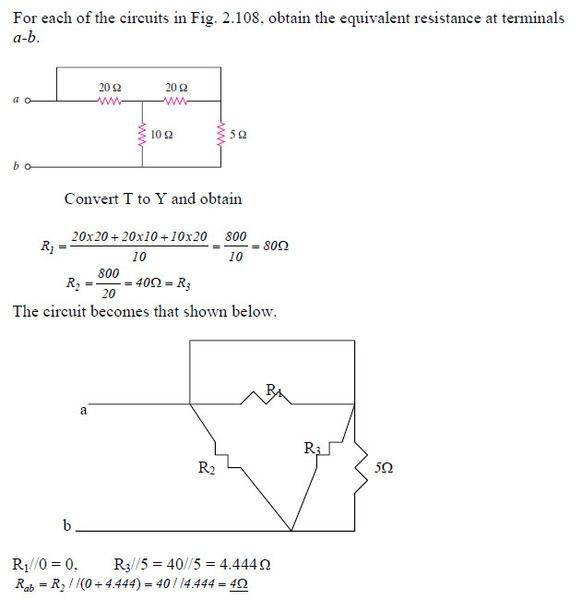
I've tried to solve using two methods above, and I've ended up with 27.14 ohm for the equivalent resistance with both methods. When I looked at the solution above, I saw that the line the two 20 ohms resistors was not ignored (I though that as long as there is not resistor in a line, it can be ignored), but instead it was assumed that there was a 0 ohm resistor.
so my questions are:
1- How does the current flows or divides in the circuit? does the current flow normally through any line even if there isn't any resistor in it?
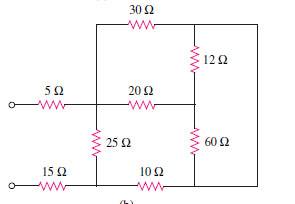
2- Is this case the same for the following?
Thank you in advance.
Anyway, this is a solved problem, but I can't get the answer :S
Homework Statement
Homework Equations
* Series-Parallel combination (RT=R1+R2+R3...+Rn for series, 1/RT=1/R1+1/R2+1/R3...+1/Rn for parallel)
* WYE (TEE) - DELTA (PI) Transformations:
1- WYE (TEE) to DELTA (PI): Each resistor in the DELTA (PI) is equal to the sum of all possible products of WYE (TEE) resistors taken two at a time, divided by the opposite WYE (TEE) resistor.
2- DELTA (PI) to WYE (TEE): Each resistor in the WYE (TEE) is equal to the product of the resistors in two adjacent DELTA (PI) branches, divided by the sum of all three DELTA (PI) resistors.
The Attempt at a Solution
I've tried to solve using two methods above, and I've ended up with 27.14 ohm for the equivalent resistance with both methods. When I looked at the solution above, I saw that the line the two 20 ohms resistors was not ignored (I though that as long as there is not resistor in a line, it can be ignored), but instead it was assumed that there was a 0 ohm resistor.
so my questions are:
1- How does the current flows or divides in the circuit? does the current flow normally through any line even if there isn't any resistor in it?
2- Is this case the same for the following?
Thank you in advance.