Wilfrid Somogyi
- 6
- 0
I'm trying to understand how to calculate the strength of the magnetic field generated by a current loop.
What I know so far is:
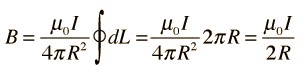
What I know so far is:
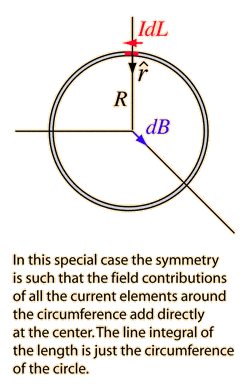
- When a current moves around a loop of wire it generates a magnetic field which looks a bit like that of a solenoid, only not so concentrated through the center of the loop.
- The magnetic field at the center of the current loop is calculated by:
- I understand what each of the terms mean except the term L and the term r (with the ^ above).
- How is this equation derived?
- What are the terms I don't recognise?
- Is there a way to calculate the magnetic field strength at any point on the plane that the loop lies in?