Current through swimmer due to lightning strike

[Ampere]

Homework Statement

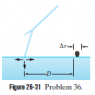
Figure 26-30 shows a swimmer at distance D=35m from a lightning strike to the water, with current I=78kA. The water has resistivity 30 Ohm*m, the width of the swimmer along a radial line from the strike is 0.7m, and his resistance across that width is 4 kOhm. Assume that the current spreads through the water over a hemisphere centered on the strike point. What is the current through the swimmer?

Homework Equations

V = IR
R = pL/A
Surface area of a hemisphere = 2*pi*r^2

The Attempt at a Solution

Assume the swimmer has a body surface area of 'A' underwater.
Then the resistance of a hypothetical 'wire' of seawater with cross-sectional area A will be p*L/A = 30*35/A

The current through this 'wire' will be the current of the lightning strike multiplied by the fraction of the surface area of the hemisphere occupied by the swimmer: Iwire = Istrike*(A/(2*pi*L^2)) = (78,000*A)/(2*pi*35^2)

The voltage applied to the swimmer is V = IR = (78,000*A*30*35)/(2*pi*35^2*A). The area of the swimmer cancels out and V is approximately 10,640 volts.

Then the current through the swimmer is I = V/R = 10,640/4000 = 2.66 A.

Did I make a mistake by not using the radial width of the swimmer? Also, my solution implies that the current through a swimmer is proportional to 1/R, where R is the distance between the swimmer and the lightning strike. Is that the right end behavior?

 

[gneill]

I think you'd want to look for the potential difference in the water between the two radii 35 m and (35 + 0.7) m. Then take ΔV/R to find the current through the swimmer.

 

[Anne Leite]

The answer for this question in the solution manual of Fundamentals of Physics (Halliday) is different, the current across the swimmer is 5.22x10^-2 A. I just didn't understand why the current is constant in a given distance r.

 

[gneill]

Hi Anne Leite, Welcome to Physics Forums!

The solution presented in your figure is making some helpful but probably unrealistic simplifications in order to make the problem tractable.

The solution assumes that the presence of the swimmer in the water isn't disturbing the hemispherical symmetry of the current radiating outward from lightning strike, that the the swimmer is somehow conforming to the hemispherical shape between two fixed radii, and that he presents a single uniform resistance.

What is assumed constant for a given radial distance is the current density, J. This corresponds to the hemispherical symmetry assumption.

 

[Anne Leite]

Hi Gneill! Why is the current density assumed to be constant at a radial distance? I didn't understand why that can be done. I know it is related to the hemispheric symmetry...

 

[gneill]

The current spreads out radially from the point of impact of the lightning strike. So the entire current is spread over the surface of a hemisphere at any given radius. Assuming that this happens symmetrically, the current density at a given radius will be a constant value over the hemispherical surface with that radius. The larger the distance, the larger hemispherical surface and the more the current is spread out (goes as the inverse square of the radius).

 

[Anne Leite]

But why can you assume it spreads symmetrically?
Sorry for the late response.

 

[gneill]

But why can you assume it spreads symmetrically?
Sorry for the late response.

Because the water represents a uniform medium. There's no preferred path; every direction in which the current can be conducted has the same resistivity. An additional assumption would be that it has zero potential at infinity.

 

[Anne Leite]

Thank you for your help.