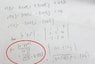chetzread
- 798
- 1
Homework Statement
[/B]
find the curvature of the vector valued function r(t) = 3sint i + 3cost j +4t k
Homework Equations
The Attempt at a Solution
For the unit tangent vector , i got T(t) = (3cost i -3sint j +4k) / sqrt (9 ((sint)^2 ) + 9 ((cost)^2 ) + 4^2 ) =
(3cost i -3sint j +4k) / 5
For the principal unit vector , N(t) , i got -3sint i -3cost j ) / sqrt (9 ((sint)^2 ) + 9 ((cost)^2 )
= -sint i -cost j
We can conclude that |r'(t) | = 5 , |T'(t) | = 3 , so , curvature = |T'(t) | / |r'(t) | = 3/5 , but the ans is 3/25 , which part of my working is wrong ?
Last edited by a moderator: