Curve C is the Common denominator of two surface

[imana41]

hi please help about this:
Curve C is the Common denominator of two surface s1:z=xy and s2:x^2+y^2-z^2=1 find Tangent vector on curve C in dot p(1,1,1) ?
i think Tangent vector on curve C is External Multiply of gradient s1 and s2 in (1,1,1)
but i get it

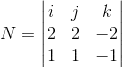=(0,0,0)

[URL]http://latex.codecogs.com/gif.latex?\bigtriangledown%20s1=(2x,2y,-2z)[/URL]
[URL]http://latex.codecogs.com/gif.latex?\bigtriangledown%20s2=(y,x,-1)[/URL]

what is my problem ?? please help

 

[HallsofIvy]

You mean "intersection" not "common denominator". Also you mean "at point p(1,1,1)" not "dot p(1,1,1)".

You have s1 and s2 reversed but yes, (2x, 2y, -2z) is normal to s2 and (y, x, -1) is normal to s1. At the given point, (1, 1, 1) those are (2, 2, -2) and (1, 1, -1). But notice that (2, 2, -2)= 2(1, 1, -1) which means the two normal vectors are parallel and the two surfaces are parallel at that point. There is no single curve of intersection at that point.

Look what happens when you try to find that curve: since z= xy, $x^2+ y^2- z^2= x^2+ y^2- x^2y^2= 1$. Then $y^2- x^2y^2= 1- x^2$, $y^2(1- x^2)= 1- x^2$ so that for any x except 1 or -1, y= 1- again there is no single intersection curve.