Curve Sketching using Data Points - Urgent Help Needed

[rum2563]

Homework Statement

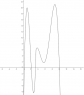
The following five points lie on a function: (1, 20), (2, 4), (5, 3), (6, 2), and (10, 1).

Find an equation which passes through these points, and which also has the following:
. . .i) three inflection points
. . .ii) at least one local maximum
. . .iii) at least one local minimum
. . .iv) at least one critical point which differs from the listed points (above)
. . .v) the property that it is continuous and differentiable throughout
. . .vi) a piecewise definition (that is, it is not a single polynomial)

Homework Equations

none

The Attempt at a Solution

Actually, can you guys help me understand the question better. Also, the fact that the graph has to be piece-wise makes it harder. Can anyone offer me a reasonable solution?

I need this urgently since it's due tomorrow. Any help would be great. Thanks.

 

[mutton]

So this is like a connect-the-dots puzzle.

You'll probably want to make each 'piece' a polynomial because it is easy to differentiate polynomials, find their max/min, etc. You know how to write a polynomial that passes through certain points. Lines are the easiest, but lines don't have local max/min. Parabolas are also easy, and they do have max/min, but no inflection points. And so on.

Where the pieces meet, you'll need to make sure that there is continuity and differentiability there. So the pieces have to 'connect', and they have to have the same slope where they meet. It is probably easiest to have slope 0 at these points, which would then have to be the max/min/inflection points.

 

[rum2563]

Thanks for your help mutton. I think I better understand the question as you have described it well. I tried doing this question into two pieces.

Please see the attached image Testnew.PNG to see if we looks ok.

Actually, when I zoom into the point (3.5,6) there is a cut in the graph which I am not sure would be ok. But I am guessing that my teacher will probably not notice it. It's after a lot of zooming that I notice the "cut" in the graph. (Please see attached zoom.png)

I really would need help in this. It's due tomorrow please. Thanks.