- #1
IronaSona
- 38
- 7
- Homework Statement
- Cut off frequency
- Relevant Equations
- 1/2*pi*L*C
How would i find the cut of frequency of this RLC circuit .I have used LTspice to find it but what is the equation for finding it
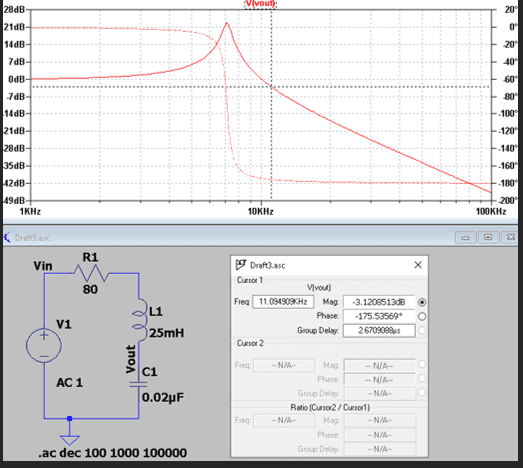
when i search it i get 1/2*pi*L*C formula , and when i use it i get answer or 8kHz but the simulation is showing 11.1kHzTSny said:Did you try a web search for "cutoff frequency LRC circuit"? For example, I found https://www.electronics-tutorials.ws/accircuits/series-resonance.html
You should look for at least one more source on the web in order to check the formulas.
##\frac{1}{2\pi\sqrt{LC}}## is the frequency of resonance, not the cutoff frequency. I suggest you read carefully the link of post #2, in post #3 I give a summary of the most important points.IronaSona said:when i search it i get 1/2*pi*L*C formula , and when i use it i get answer or 8kHz but the simulation is showing 11.1kHz
what is the w is that the 2*piDelta2 said:It depends how you define the cut off frequency. The article given in the link of post #2 defines the cutoff frequency as the frequency (of the source) that the amplitude of the current in the circuit is equal to 70.7% of its maximum(resonant) value. There are two possible values of reactance ##X=\omega L-\frac{1}{\omega C}## to realize this current , ##X=-R## and ##X=R##. Solving $$-R=\omega_1L-\frac{1}{\omega_1 C}$$ gives the lower cutoff frequency ##\omega_1## and solving $$R=\omega_2L-\frac{1}{\omega_2 C}$$ gives the higher cutoff frequency ##\omega_2##
##\omega## is the angular frequency is is equal to ##\omega=2\pi f## where ##f## the frequencyIronaSona said:what is the w is that the 2*pi
o ok thank youDelta2 said:##\omega## is the angular frequency is is equal to ##\omega=2\pi f## where ##f## the frequency
thank you , ill try it .TSny said:As @Delta2 pointed out, the link in post #2 is for the case where you are looking at the output voltage across the resistor instead of the capacitor. So, that link does not give the formula for the cutoff frequency for your situation.
As @DaveE noted in the previous post, finding the -3dB cutoff frequency involves solving the quadratic equation that he wrote down. The solution is a little messy. (I let Mathematica find it!)
$$f_{\rm c.o.} = \frac{1}{2\pi}\left[\frac{1}{LC} - \frac{R^2}{2L^2}+\sqrt{\frac{2}{L^2C^2}-\frac{R^2}{L^3C}+\frac{R^4}{4L^4}} \right]^{1/2}$$ You can plug in your values for ##R, L## and ##C## to see if you get a cutoff frequency of about 11 kHz.
The cutoff frequency for an RLC circuit is the frequency at which the circuit begins to attenuate or block certain frequencies of the input signal. It is also known as the corner frequency or half-power frequency.
The cutoff frequency can be calculated using the formula fc = 1/(2π√(LC)), where fc is the cutoff frequency, L is the inductance of the circuit, and C is the capacitance of the circuit.
The cutoff frequency is an important parameter in an RLC circuit as it determines the range of frequencies that the circuit can effectively filter or pass through. It also helps in designing and analyzing the performance of the circuit.
The cutoff frequency affects the output of an RLC circuit by attenuating or blocking certain frequencies of the input signal. As the frequency of the input signal approaches the cutoff frequency, the output signal will decrease in amplitude.
The cutoff frequency of an RLC circuit can be affected by the values of the inductance and capacitance components, as well as the resistance of the circuit. Changes in these values can result in a different cutoff frequency and alter the performance of the circuit.