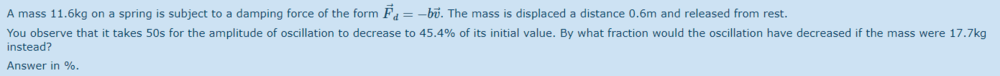Dampening force - find decrease in amplitude

In summary, dampening force is a force that opposes the motion of an object and causes it to lose energy and decrease in amplitude over time. It is typically measured in units of Newtons (N) or Joules per meter (J/m) and is affected by factors such as the mass of the object, its speed of motion, and the properties of the medium it is moving through. The decrease in amplitude can be calculated using the equation A = A<sub>0</sub>e<sup>-bt</sup>, where A<sub>0</sub> is the initial amplitude, b is the dampening coefficient, and t is time. To reduce the effect of dampening force, one can use materials with lower dampening
  • #1
JoeyBob
256
29
Homework Statement
see attached
Relevant Equations
w=sqrt((k/m)-(b/(2m))^2)

Amplitude = (Amax)e^((-b/(2m)t)
So first I tried to find b.

0.454=(0.6)e^((-b/(2*11.6)*50)

Anyways with some natural log algebra etc. I get b = 0.129378

But when I plug this into the same equation only changing mass to 17.7 kg I get 0.4998 or 50% when the answer should be 59.6%?
 

Attachments

  • question.PNG
    question.PNG
    8 KB · Views: 102
Physics news on Phys.org
  • #2
JoeyBob said:
Amplitude = (Amax)e^((-b/(2m)t)

0.454=(0.6)e^((-b/(2*11.6)*50)
The amplitude decreases to 45.4% of its initial value. So, the final amplitude is not .454
 

FAQ: Dampening force - find decrease in amplitude

What is dampening force?

Dampening force is a type of force that acts to decrease the amplitude of an oscillating system. It is usually caused by friction or resistance within the system.

How does dampening force affect the amplitude of an oscillating system?

Dampening force decreases the amplitude of an oscillating system over time. As the system continues to oscillate, the dampening force acts against the motion, causing it to gradually lose energy and decrease in amplitude.

How can you find the decrease in amplitude caused by dampening force?

To find the decrease in amplitude caused by dampening force, you can use the equation A = A0e-bt, where A is the amplitude at a given time t, A0 is the initial amplitude, and b is the dampening coefficient. By plugging in different values for t, you can calculate the decrease in amplitude over time.

Can dampening force ever increase the amplitude of an oscillating system?

No, dampening force always acts to decrease the amplitude of an oscillating system. It works against the motion and causes the system to lose energy, resulting in a decrease in amplitude.

How can you reduce the effects of dampening force on an oscillating system?

One way to reduce the effects of dampening force on an oscillating system is to decrease the amount of friction or resistance within the system. This can be achieved by using smoother surfaces or lubricants to reduce friction, or by using materials with lower resistance. Another way is to increase the energy input into the system, which can counteract the effects of dampening force and maintain a higher amplitude.

Similar threads

Textbook 'The Physics of Waves': Varying Force Amplitude
Replies
3
Views
443
Difference between resonance in undamped vs damped mass-spring-dashpot
Replies
17
Views
1K
Mass atop four springs with external input: Reduce vibration amplitude by factor of ten
Replies
3
Views
430
Damped harmonic oscillation of a swingboat
Replies
6
Views
1K
Change in the amplitude of a damped spring block oscillator
Replies
1
Views
1K
Finding Amplitude of spring oscillation after damping
Replies
15
Views
4K
Why does a capacitor decrease current amplitude
Replies
4
Views
3K
Is internal energy really decreasing in situation 2?
Replies
32
Views
2K
Find the maximum amplitude of the induced EMF
Replies
9
Views
6K
Shm , calculation of amplitude of spring mass system
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top