Smooth
- 6
- 3
Hi,
I need something that would measure vibrations along an axis, so instead of buying a bunch of accelerometers I thought I’d quickly make smth myself. I’m majoring in engineering and not physics, so while I have no problems with the construction, I’m kind of stuck with the physics aspect.
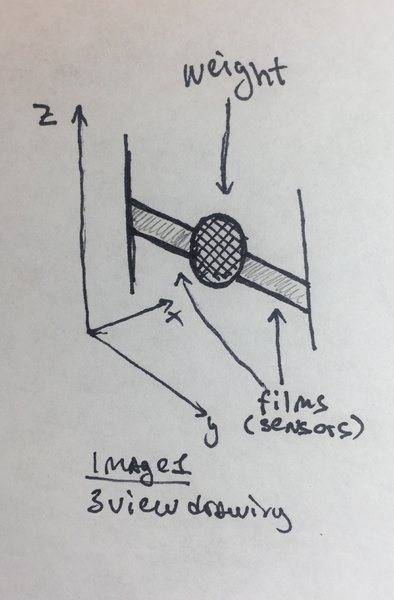
I explained my device on image 1. I have a weight that is suspended by two films (flex sensors - Piezo vibration). When a vibration along the x-axis is introduced, the weight will deviate and oscillate a little until coming back to initial position.
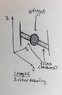
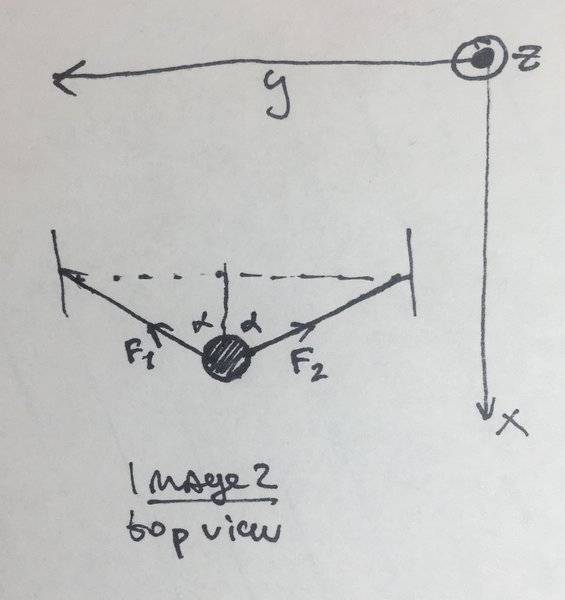
The graphic is on image 2. Suppose the weight deviates from original position. I will have the returning forces of tension from the films, and since I know the Young’s modulus of the films I can calculate the tension force due to the films. I wrote the 2nd Newton’s law on image 3.
Now, here’s my question; how do I factor in air resistance/damping of this half-pendulum? Yeah, I can easily get it experimentally by graphing the waveform. But can I write equations though?
I’ll probably increase the surface area of the weight to increase air resistance and play around with its mass to increase the damping, but question remains - how do theoretically predict that damping effect?
Many thanks for any suggestions.

I need something that would measure vibrations along an axis, so instead of buying a bunch of accelerometers I thought I’d quickly make smth myself. I’m majoring in engineering and not physics, so while I have no problems with the construction, I’m kind of stuck with the physics aspect.
I explained my device on image 1. I have a weight that is suspended by two films (flex sensors - Piezo vibration). When a vibration along the x-axis is introduced, the weight will deviate and oscillate a little until coming back to initial position.
The graphic is on image 2. Suppose the weight deviates from original position. I will have the returning forces of tension from the films, and since I know the Young’s modulus of the films I can calculate the tension force due to the films. I wrote the 2nd Newton’s law on image 3.
Now, here’s my question; how do I factor in air resistance/damping of this half-pendulum? Yeah, I can easily get it experimentally by graphing the waveform. But can I write equations though?
I’ll probably increase the surface area of the weight to increase air resistance and play around with its mass to increase the damping, but question remains - how do theoretically predict that damping effect?
Many thanks for any suggestions.