Dealing with Undefined Values in Calculus: A Lesson in Limits

[archaic]

Homework Statement

N/A

Relevant Equations

N/A

This is not to ask for a solution, rather I want comments on the rigor of the step. Thank you for your time!

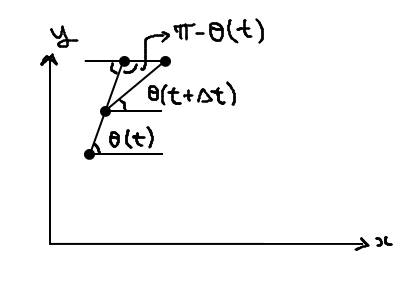
The graph shows a system of two points at $t$ and $t+dt$, it is a bit exaggerated of course.
The upper point is moving strictly in the $x$ direction and has a constant velocity $u$, while the lower point is always moving towards the upper point with constant velocity $v>u$. I want to find the rate of change of the distance $\mathcal{L}(t)$ which separates them (to find the time of collision $\tau$).

Keeping in mind that $\cos(\pi-\theta)=-\cos(\theta)$ and the cosines' law:
$$\begin{align*}
\mathcal{L}^2(t+\Delta t)&\approx(u\Delta t)^2+(\mathcal{L}(t)-v\Delta t)^2+2(u\Delta t)(\mathcal{L}(t)-v\Delta t)\cos(\theta(t))\\
&\approx(u\Delta t)^2+\mathcal{L}^2(t)-2v\mathcal{L}(t)\Delta t+(v\Delta t)^2+2u\mathcal{L}(t)\cos(\theta(t))\Delta t-2uv\cos(\theta(t))(\Delta t)^2
\end{align*}$$
$$\begin{align*}
\mathcal{L}^2(t+\Delta t)-\mathcal{L}^2(t)&\approx(u\Delta t)^2-2v\mathcal{L}(t)\Delta t+(v\Delta t)^2+2u\mathcal{L}(t)\cos(\theta(t))\Delta t-2uv\cos(\theta(t))(\Delta t)^2\\
\frac{\mathcal{L}^2(t+\Delta t)-\mathcal{L}^2(t)}{\Delta t}&\approx u^2\Delta t-2v\mathcal{L}(t)+v^2\Delta t+2u\mathcal{L}(t)\cos(\theta(t))-2uv\cos(\theta(t))\Delta t
\end{align*}$$
Now let $\Delta t\to 0$, we have:
$$\begin{align*}
\frac{d}{dt}\mathcal{L}^2(t)&=-2v\mathcal{L}(t)+2u\mathcal{L}(t)\cos(\theta(t))\\
\Leftrightarrow 2\mathcal{L}(t)\mathcal{L}'(t)&=-2v\mathcal{L}(t)+2u\mathcal{L}(t)\cos(\theta(t))\\
\Leftrightarrow \mathcal{L}'(t)&=-v+u\cos(\theta(t))
\end{align*}$$
My problem is here, when $t=\tau$, $\mathcal{L}(\tau)=\mathcal{L}'(\tau)=0$ and the division is then undefined. How can I go around this?

 

[Mark44]

... and the division is then undefined

I don't see this as a problem. In the definition of the derivative of f at a point x₀, you have this limit:
$$\lim_{h \to 0}\frac{f(x_0 + h) - f(x_0)} h$$
When h = 0, the fraction is undefined, but that is the whole idea of defining the derivative in terms of a limit.

 

[archaic]

I don't see this as a problem. In the definition of the derivative of f at a point x₀, you have this limit:
$$\lim_{h \to 0}\frac{f(x_0 + h) - f(x_0)} h$$
When h = 0, the fraction is undefined, but that is the whole idea of defining the derivative in terms of a limit.

Oh no, not that. I'am talking about the division by the length in the last step.

 

[Mark44]

Your equation will be valid as $\mathcal L (t)$ approaches 0.

 

[archaic]

Your equation will be valid as $\mathcal L (t)$ approaches 0.

How can I have a definite answer then? If I consider the simplification true when $t=\tau$, the answer is correct.

 

[Mark44]

Your question seems to me to be similar to this:
If $f(x) = \frac{x^2 - 1}{x - 1}$, what is f(1)?
Well, f(1) is undefined, because both numerator and denominator are zero when x = 1.
But, by using limits, we can determine that $\lim_{x \to 1} = \lim_{x \to 1}\frac{x^2 - 1}{x - 1} = \lim_{x \to 1} \frac{(x - 1)(x + 1)}{x - 1} = \lim_{x \to 1}x + 1 = 2$.
Clearly if x = 1, cancalling x - 1 from numerator and denominator isn't valid, but for any other value of x, $\frac{(x - 1)(x + 1)}{x - 1} = x + 1$

 

[archaic]

Your question seems to me to be similar to this:
If $f(x) = \frac{x^2 - 1}{x - 1}$, what is f(1)?
Well, f(1) is undefined, because both numerator and denominator are zero when x = 1.
But, by using limits, we can determine that $\lim_{x \to 1} = \lim_{x \to 1}\frac{x^2 - 1}{x - 1} = \lim_{x \to 1} \frac{(x - 1)(x + 1)}{x - 1} = \lim_{x \to 1}x + 1 = 2$.
Clearly if x = 1, cancalling x - 1 from numerator and denominator isn't valid, but for any other value of x, $\frac{(x - 1)(x + 1)}{x - 1} = x + 1$

i.e the "correct" way to answer the problem is by canceling inside the limit.