SUMMARY
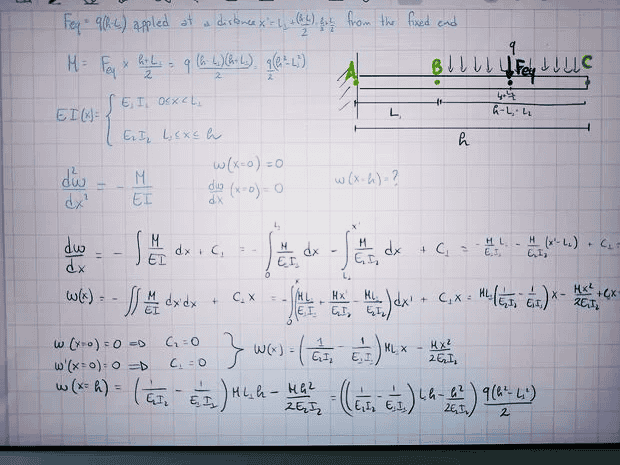
The discussion focuses on calculating the deflection of a cantilever beam with a fixed end, subjected to a uniform load. The beam has a rectangular cross-section and varies in material properties, specifically the modulus of elasticity (E) and moment of inertia (I), across two segments: 0 < x ≤ L and L < x ≤ 0. The governing differential equations for deflection are established as $$\frac{d^2y}{dx_1^2} = \frac{M_1(x_1)}{E_1I_1}$$ and $$\frac{d^2y}{dx_2^2} = \frac{M_2(x_2)}{E_2I_2}$$. The constants of integration for each segment are determined by the boundary conditions at the fixed end.
PREREQUISITES
- Understanding of beam theory and deflection analysis
- Familiarity with differential equations in structural mechanics
- Knowledge of material properties such as modulus of elasticity (E) and moment of inertia (I)
- Ability to calculate internal moments and reactions in beams
NEXT STEPS
- Learn how to derive the internal moment equations for cantilever beams under uniform loads
- Study the method of superposition for analyzing non-homogeneous beams
- Explore numerical methods for solving differential equations in structural analysis
- Investigate software tools like MATLAB or ANSYS for simulating beam deflection
USEFUL FOR
Structural engineers, mechanical engineers, and students studying beam mechanics will benefit from this discussion, particularly those focused on analyzing cantilever beams with variable material properties.