Depth of a basketball floating on water

[brotherbobby]

Homework Statement

A basketball of mass 600 g and radius 12 cm floats at rest on the surface of water. Calculate the depth $\boldsymbol{d}$ of the ball that's under the liquid surface.

Relevant Equations

(1) Law of floatation : The mass of a floating body is the mass of liquid displaced - $m_B=\Delta m_L$.
(2) Equation of a spherical surface : $x^2+y^2+z^2=a^2$, where $a$ is the radius.

Attempt : (Turns out, there is more mathematics in this problem than physics. The crucial part involves the use of vector calculus where one needs to find the volume of a region bounded at the top by a portion of a sphere. That is where am stuck.)

The mass of water displaced by the ball $\Delta m = 0.6\;\text{kg}$. This amounts to the volume of liquid displaced : $\Delta V_L = 600\;\text{cm}^3$. This is also the volume of the ball inside liquid : $\Delta V_B = 600\;\text{cm}^3$.

$\text{The question is - how to relate this volume to the depth inside liquid?}$

I make a sketch of the problem situation. I need to find the depth inside water $d=?$

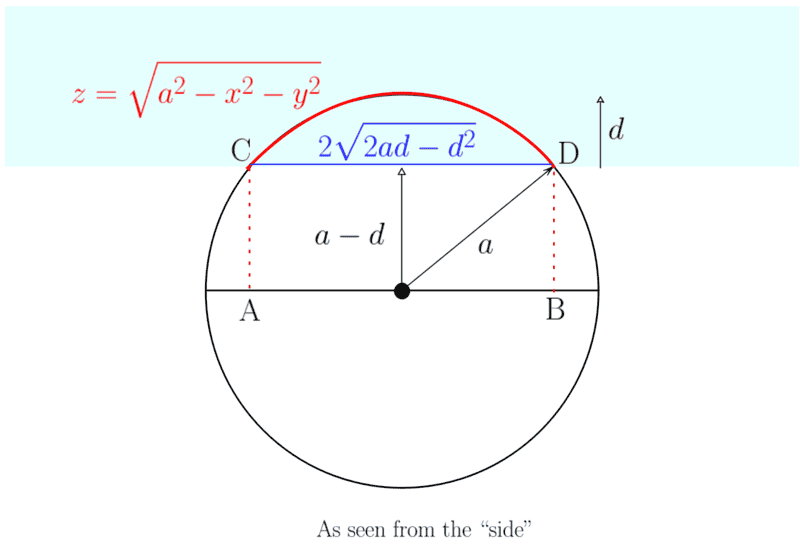If I "overturn" the basketball and looking from the "side", call its radius as $a$, I would have an image like the one alongside. The red arc $\color{red}{\stackrel{\large{\frown}}{CD}}$ is the 2-D surface of the ball inside water whose $(x,y,z)$ coordinates at any point are related by $z=\sqrt{a^2-x^2-y^2}$. The blue line $\color{blue}{\overline{CD}}$ marks the boundary of the region under water. Using the Pythagorean theorem, the length of the line ${\color{blue}{\overline{CD}}}\text{AB}$ is $2\sqrt{2ad-d^2}$. We understand that this line ${\color{blue}{\overline{CD}}}\text{AB}$ is the diameter of the circle at the boundary of liquid.


Hence the volume of the region under water is the difference of the volume of region ${\color{red}{\stackrel{\large{\frown}}{CD}}}\text{AB}$ and ${\color{blue}{\overline{CD}}}\text{AB}$.

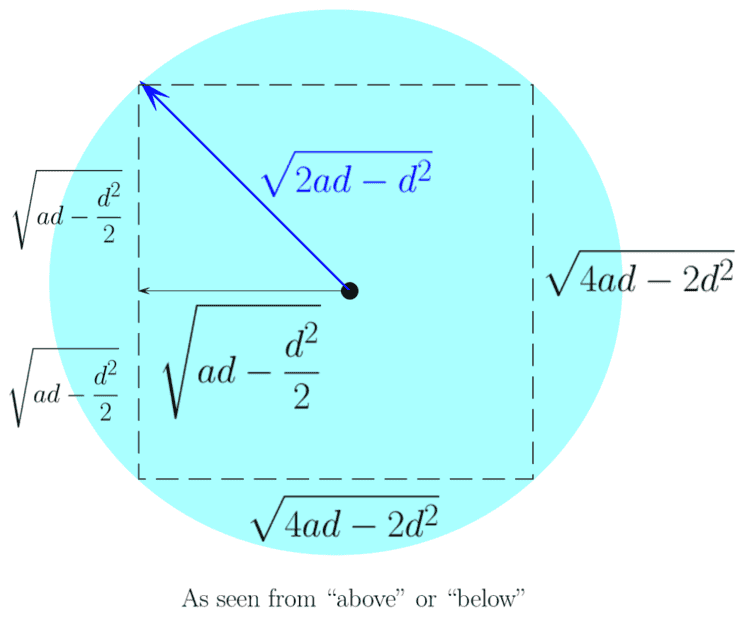The volume of the region ${\color{blue}{\overline{CD}}}\text{AB}$ is easy. It is a cuboid with a square on "top" of dimensions $\sqrt{4ad-2d^2}$, calculated upon use of the Pythagorean theorem to find the side of a square given its radius (= $\sqrt{2ad-d^2}$). The height of the cudoid (as seen from the "side") is $(a-d)$. Hence the volume of the cuboid ${\color{blue}{\overline{CD}}}\text{AB}$ is : $V_{\text{cuboid}}=2(2ad-d^2)(a-d)$.

But now to find the volume of the region ${\color{red}{\stackrel{\large{\frown}}{CD}}}\text{AB}$ whose upper serface is a portion of a sphere?

This is where am stuck. I am aware that the equation of the upper surface $\color{red}{\stackrel{\large{\frown}}{CD}}$ is $\color{red}{z=\sqrt{a^2-x^2-y^2}}$. The lower surface of the same region is a square of dimensions $\sqrt{4ad-2d^2}$. But how to find its volume?


Given my lack of progress on this crucial but elementary point, any hint would be welcome.

 

[haruspex]

Divide the submerged region into horizontal discs. If the ball has radius r and a disc thickness dx is distance x from the ball's centre, what, approximately, is its volume?

Btw, there is only one "a" in "flotation".

 

[brotherbobby]

Divide the submerged region into horizontal discs. If the ball has radius r and a disc thickness dx is distance x from the ball's centre, what, approximately, is its volume?

Btw, there is only one "a" in "flotation".

Yes, I can do the problem that way. I do it below roughly writing into $\text{Sketchbook}^{\circledR}$ and hope it's readable.

We end up with a cubic equation we have to solve to find $d$ : $d^3-0.36d^2-5.73\times 10^{-4}=0$.

Since I don't know how to solve it, let me try online.

The answer comes out to be : $\boxed{d = 4.2\;\text{cm}}$.

 

[brotherbobby]

The question is, can this be done in the way I wanted to do in post #1, taking the equation of a sphere and subtracting volumes of regions to find the volume enclosed.

 

[haruspex]

The question is, can this be done in the way I wanted to do in post #1, taking the equation of a sphere and subtracting volumes of regions to find the volume enclosed.

If one method leads to having to solve a cubic, and that cubic has no rational solution, then all solutions will lead to that.

 

[haruspex]

$d$ : $d^3-0.36d^2-5.73\times 10^{-4}=0$.

Sign error, but I'm guessing it’s just a typo.

 

[brotherbobby]

Sign error, but I'm guessing it’s just a typo.

Yes, it was a typo. The answer $\boxed{d = 4.2\;\text{cm}}$ correct.

If one method leads to having to solve a cubic, and that cubic has no rational solution, then all solutions will lead to that.

I agree, but I still want to solve it that way.

It's a bit like finding the volume of a sphere. You can break the sphere into concentric shells of radius $x$ and thickness ${\rm{d}} x$ : $$V = \int\limits_0^a 4\pi x^2 dx$$.
You can also use the equation of a sphere ($x^2+y^2+z^2=a^2$) and solve the triple integral finding volume : $$V=\int\limits_{-a}^{+a}dx \int\limits_{-\sqrt{a^2-x^2}}^{+\sqrt{a^2-x^2}}dy \int\limits_{-\sqrt{a^2-x^2-y^2}}^{+\sqrt{a^2-x^2-y^2}}dz$$
(Stuck though I am, I'd like to do it in the second way to see if I get the same answer)

 

[brotherbobby]

I am afraid to bring you back @haruspex to the (unsolved) problem above of finding the volume of the spherical cap , at least the way I'd want it. Forget the numerical details for now.

The goal : $\textbf{To calculate the volume of the spherical dome using the method of calculus.}$

Now I succeeded in doing that using the method you said in post #2, using thin discs of thickness $dx$ at distances of (increasing) $x$ from the sphere's center. The answer came out to be $\boxed{V = \dfrac{\pi d^2}{3}(\underline{3}a-d)}\qquad (1)$. I underline the 3 for a reason that will be apparent soon.

But why only the center? What if I wanted to choose a point at the base of the dome and move increasingly to its north pole?

Below is a sketch of what I have in mind.

Let's focus on the spherical cap. The volume of the thin disc is $dV = \pi r^2(x) dx$, where the radius of the disc $r(x)= \frac{b}{d}x$, using the method of similar triangles.

Thus the volume of the dome $V= \dfrac{\pi b^2}{d^2}\int\limits_0^d x^2\;dx= \dfrac{\pi b^2}{d^2}\dfrac{d^3}{3}=\dfrac{\pi d}{3} (2ad-d^2)=\dfrac{\pi d^2}{3}(\underline{2}a-d)\qquad (2)$.

As you will note, the coefficient of a underlined in the brackets is 2 , different from the correct expression in (1) above which is 3.

Request : I'd be glad if you told me what's the error in my calculation.

 

[Hill]

what's the error in my calculation

This:

Because the triangles $r/x$ and $b/d$ are not similar.

 

[brotherbobby]

Because the triangles r/x and b/d are not similar.

Thank you. Sorry I got betrayed by the looks.