Derivation of the CHSH inequality

[Alien8]

Bell's 1971 derivation
The following is based on page 37 of Bell's Speakable and Unspeakable (Bell, 1971), the main change being to use the symbol ‘E’ instead of ‘P’ for the expected value of the quantum correlation. This avoids any implication that the quantum correlation is itself a probability.

We start with the standard assumption of independence of the two sides, enabling us to obtain the joint probabilities of pairs of outcomes by multiplying the separate probabilities, for any selected value of the "hidden variable" λ. λ is assumed to be drawn from a fixed distribution of possible states of the source, the probability of the source being in the state λ for any particular trial being given by the density function ρ(λ), the integral of which over the complete hidden variable space is 1. We thus assume we can write:

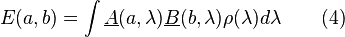
where A and B are the average values of the outcomes. Since the possible values of A and B are −1, 0 and +1, it follows that:

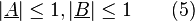
Then, if a, a′, b and b′ are alternative settings for the detectors,

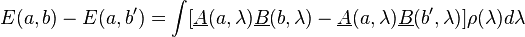
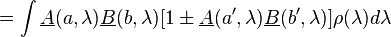
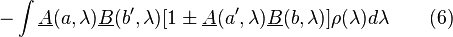
Then, applying the triangle inequality to both sides, using (5) and the fact that

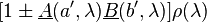as well as

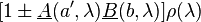are non-negative we obtain

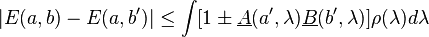
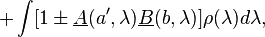
or, using the fact that the integral of ρ(λ) is 1,

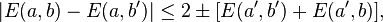
which includes the CHSH inequality.
--- END QUOTE
http://en.wikipedia.org/wiki/CHSH_inequality#Derivation_of_the_CHSH_inequality1. "We start with the standard assumption of independence of the two sides, enabling us to obtain the joint probabilities of pairs of outcomes by multiplying the separate probabilities..."

Obtain the joint probability of what particular event?2. We see the premise from step (5) applied in step (6) which adds that $\pm 1$ into the equation, but without it, what is the underlying relation between four expectation values the equation describes? Would it be this: $E(a,b) - E(a,b') = E(a,b) * E(a',b') - E(a,b') * E(a',b)$?3. Step after (6), applying the triangle inequality to both sides. What is justification for this?

 

[Alien8]

Step 6.

In that step, the idea they are using is that $A = B + C$ can also be written as $A = B + C + D - D$. Basically we can add any term that is of the form $D - D$ since $D - D = 0$.

There is E(a,b), E(a,b′), E(a′,b) and E(a′,b′), which I will call E1, E2, E3 and E4. Is that what you call A, B, C and D, so that: E1 = E2 + E3 + E4 - E4?

 

[atyy]

There is E(a,b), E(a,b′), E(a′,b) and E(a′,b′), which I will call E1, E2, E3 and E4. Is that what you call A, B, C and D, so that: E1 = E2 + E3 + E4 - E4?

The term I'm calling $D$ is $\underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda)$.

The term in the square brackets in the integrand is:
$\underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)\underline{A}(a',\lambda)\underline{B}(b,\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)\underline{A}(a',\lambda)\underline{B}(b,\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda)[1 + \underline{A}(a',\lambda)\underline{B}(b',\lambda)] - \underline{A}(a,\lambda)\underline{B}(b',\lambda)[1+ \underline{A}(a',\lambda)\underline{B}(b,\lambda)]$

 

[Alien8]

The term I'm calling $D$ is $\underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda)$.

The term in the square brackets in the integrand is:
$\underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)\underline{A}(a',\lambda)\underline{B}(b,\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda) + \underline{A}(a,\lambda)\underline{B}(b,\lambda)\underline{A}(a',\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda) - \underline{A}(a,\lambda)\underline{B}(b',\lambda)\underline{A}(a',\lambda)\underline{B}(b,\lambda)$
$= \underline{A}(a,\lambda)\underline{B}(b,\lambda)[1 + \underline{A}(a',\lambda)\underline{B}(b',\lambda)] - \underline{A}(a,\lambda)\underline{B}(b',\lambda)[1+ \underline{A}(a',\lambda)\underline{B}(b,\lambda)]$

So looking just at the equation in the first two lines, and given:

$\int \underline{A}(a,\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a,b) = E1$
$\int \underline{A}(a,\lambda)\underline{B}(b',\lambda) \rho( \lambda ) d\lambda = E(a,b') = E2$
$\int \underline{A}(a',\lambda)\underline{B}(b',\lambda) \rho( \lambda ) d\lambda = E(a',b') = E3$
$\int \underline{A}(a',\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a',b) = E4$

then in the original terms of expectation values it goes like this:

$E1 - E2 = E1-E2 + E1*E3 - E1*E4$

Correct? The question is where did that come from, according to what premise or mathematical principle is it supposed to be true? What is it E1, E2, E3 and E4 have in common to justify such a statement about their shared relationship? How do you prove that equation is true? Is it supposed to be true only for QM, only classical physics, or both?

 

[atyy]

So looking just at the equation in the first two lines, and given:

$\int \underline{A}(a,\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a,b) = E1$
$\int \underline{A}(a,\lambda)\underline{B}(b',\lambda) \rho( \lambda ) d\lambda = E(a,b') = E2$
$\int \underline{A}(a',\lambda)\underline{B}(b',\lambda) \rho( \lambda ) d\lambda = E(a',b') = E3$
$\int \underline{A}(a',\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a',b) = E4$

then in the original terms of expectation values it goes like this:

$E1 - E2 = E1-E2 + E1*E3 - E1*E4$

Correct?

No, that is not right. Don't think about the expectation values, just the term in the square brackets of the integrand.

$\underline{A}(a,\lambda)\underline{B}(b,\lambda) = D1$
$\underline{A}(a,\lambda)\underline{B}(b',\lambda) = D2$
$\underline{A}(a',\lambda)\underline{B}(b',\lambda) = D3$
$\underline{A}(a',\lambda)\underline{B}(b,\lambda) = D4$

Then the original term can be rewritten:

$D1 - D2 = D1-D2 + D1*D3 - D1*D3$

 

[billschnieder]

$\underline{A}(a,\lambda)\underline{B}(b,\lambda) = D1$
$\underline{A}(a,\lambda)\underline{B}(b',\lambda) = D2$
$\underline{A}(a',\lambda)\underline{B}(b',\lambda) = D3$
$\underline{A}(a',\lambda)\underline{B}(b,\lambda) = D4$

Then the original term can be rewritten:

$D1 - D2 = D1-D2 + D1*D3 - D1*D3$

Paraphrasing Alien8, one could ask the same question about D1, D2, D3, and D4:

The question is where did that come from, according to what premise or mathematical principle is it supposed to be true? What is it D1, D2, D3 and D4 have in common to justify such a statement about their shared relationship? How do you prove that equation is true? Is it supposed to be true only for QM, only classical physics, or both?

 

[Alien8]

Paraphrasing Alien8, one could ask the same question about D1, D2, D3, and D4:

The question is where did that come from, according to what premise or mathematical principle is it supposed to be true?

We are back talking about relations between binary states instead of expectation values, even though they do not compare. Just like AB + AB' + A'B - A'B' = -2 or +2, that equation too is true according to pure algebra involving specifically numbers -1 and +1. There seem to be many combinations of arithmetic operations involving four variables with {-1,+1} limit that will yield equality, in which case the choice of that particular expression is simply arbitrary.

What is it D1, D2, D3 and D4 have in common to justify such a statement about their shared relationship?

The only thing they have in common is their limit {-1,+1}. But that is sufficient to construct numerous combinations of general algebraic equalities concerning four independent arbitrary variables with such a limit.

How do you prove that equation is true?

I evaluated the equation several times, each time assigning arbitrarily different -1 or +1 values to D variables. The equation produced 0 = 0, -2 = -2, and 2 = 2 results.

There seems to be an error in the third line though, which involves all four variables: D1-D2 = D1-D2 + D1*D3 - D2*D4 and it's true only for some combinations.

Is it supposed to be true only for QM, only classical physics, or both?

It's true for every possible combination of four variables under condition each one can be only -1 or +1. It's general and purely mathematical statement about numbers, it has no more to do with QM than 1 + 1 = 2.

 

[atyy]

There seems to be an error in the third line though, which involves all four variables: D1-D2 = D1-D2 + D1*D3 - D2*D4 and it's true only for some combinations.

Yes, if you assign the values D1,D2,D3,D4 with no relation between them (except that they have the same limits), then you will get an error in the third line. However, D1*D3 is not independent from D2*D4. In fact D1*D3 = D2*D4, because D1*D3 and D2*D4 are made up of the same "A" and "B" terms written in different orders.

So if you want to assign values between -1 and +1 independently to check the equation, you should assign them to the "A" and "B" terms.

 

[Alien8]

No, that is not right. Don't think about the expectation values, just the term in the square brackets of the integrand.

$\underline{A}(a,\lambda)\underline{B}(b,\lambda) = D1$
$\underline{A}(a,\lambda)\underline{B}(b',\lambda) = D2$
$\underline{A}(a',\lambda)\underline{B}(b',\lambda) = D3$
$\underline{A}(a',\lambda)\underline{B}(b,\lambda) = D4$

If you lose the integral you don't have a number any more, but a binary state which is not a subject to arithmetic operations: dead & alive - alive & alive is undefined, it does not compute. That a photon goes one way or the other has no numerical value, it's an event or state. Assigning -1 and +1 labels to a binary state is very peculiar choice because it can obviously be misleading.

In any case, those D variables do not represent numbers, but four possible binary states or events: $(++), (--), (+-), (-+)$. We can't do arithmetic with that, we need to count occurrences of many such events in order to work out probabilities and expectation values, and then we get the numbers we can actually do arithmetic with.

Then the original term can be rewritten:

$D1 - D2 = D1-D2 + D1*D3 - D1*D3$

Relation between independently arbitrary binary states is not relevant to expectation values. That two coins can either flip heads or tails has nothing to with how often they will both flip the same side. The derivation never looses the integral, expectation values E1 - E2 always remain on the left hand side of the equation. The equation ought to able to be expressed only in terms of expectation values, which is what the derivation begins and ends up with anyway.

 

[Avodyne]

If you lose the integral you don't have a number any more, but a binary state which is not a subject to arithmetic operations

In hidden variable theory, you do have a number that is subject to arithmetic operations. That is the whole point of hidden variable theory.

If you deny that $D1$ is a definite number (which must be either $+1$ or $-1$), then you are outside the framework of hidden variable theory, and the Bell inequalities cannot be derived.

The Bell inequalities apply only to local hidden variable theories, which are defined to be those theories in which $A(a,\lambda)$, etc., have definite values (either $+1$ or $-1$) for each value of the hidden variable $\lambda$.

The Bell inequalities do not apply to any theory in which $A(a,\lambda)$ does not have a definite value (either $+1$ or $-1$) for each value of the hidden variable $\lambda$.

One such theory is quantum mechanics.

 

[Alien8]

If you deny that $D1$ is a definite number (which must be either $+1$ or $-1$), then you are outside the framework of hidden variable theory, and the Bell inequalities cannot be derived.

I don't deny that, I observe that for probabilities and expectation values it is irrelevant whether the four possible events will be labeled ++, --, +-, -+ or 11, 00, 10, 01 or HH, TT, HT, TH, or whatever other binary state label with the Boolean domain. It's probability of those events happening which has a definite decimal range from 0.0 to 1.0, and it's expectation values which have definite decimal range from -1.0 to +1.0.

By the way, boolean logic operations do not directly translate to numbers arithmetic, and the outcome sample space always has the same boundary as input Boolean domain: {true, false}.

The Bell inequalities apply only to local hidden variable theories, which are defined to be those theories in which $A(a,\lambda)$, etc., have definite values (either $+1$ or $-1$) for each value of the hidden variable $\lambda$.

The Bell inequalities do not apply to any theory in which $A(a,\lambda)$ does not have a definite value (either $+1$ or $-1$) for each value of the hidden variable $\lambda$.

The Bell inequality I quoted in the OP is not about binary states like: $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ , but about expectation values such as: $\int \underline{A}(a,\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a,b)$. Some people seems to think relations between binary state events are directly consequential to expectation values, but they are general and only define input domain limit, it's always the same for any theory you want to test the inequality against, and how the inequality will evaluate only depends on expectation value function or "hidden variable".

 

[Avodyne]

The Bell inequality I quoted in the OP is not about binary states like: $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ , but about expectation values such as: $\int \underline{A}(a,\lambda)\underline{B}(b,\lambda) \rho( \lambda ) d\lambda = E(a,b)$.

Sure, but you prove the Bell inequality for $E(a,b)$ by using properties of $\underline{A}(a,\lambda)$.

Consider a particular combination of expectation values, $E(a,b)+E(a,b')+E(a',b)-E(a',b')$. In local hidden variable theory, this combination can be written as

$E(a,b)+E(a,b')+E(a',b)-E(a',b')={}$
$\int\left[ \underline{A}(a,\lambda)\underline{B}(b,\lambda) +\underline{A}(a,\lambda)\underline{B}(b',\lambda) +\underline{A}(a',\lambda)\underline{B}(b,\lambda) -\underline{A}(a',\lambda)\underline{B}(b',\lambda)\right]\!\rho(\lambda)d\lambda$

where $\underline{A}(a,\lambda)$, etc., are each equal to $+1$ or $-1$. (This is simply how we are choosing to represent the two binary values. This choice implies $-1\le E(a,b)\le +1$.)

Do you agree with this, or not?

 

[Alien8]

Sure, but you prove the Bell inequality for $E(a,b)$ by using properties of $\underline{A}(a,\lambda)$.

$\underline{A}(a,\lambda)$ is unknown function with output sample space: {event 1, event 2}. This output is then only a part of the input for expectation value function. Event naming is arbitrary, probability only cares about the count or ratio of their occurrences.

where $\underline{A}(a,\lambda)$, etc., are each equal to $+1$ or $-1$. (This is simply how we are choosing to represent the two binary values. This choice implies $-1\le E(a,b)\le +1$.)

Do you agree with this, or not?

Expectation value is measure of probabilities between four possible events. Probabilities naturally range from 0.0 to 1.0, so the reason why expectation values range from -1.0 to +1.0 is because: $E(a,b) = P_{++}(a,b) + P_{--}(a,b) − P_{+-}(a,b) − P_{-+}(a,b)$.

 

[atyy]

$\underline{A}(a,\lambda)$ is unknown function with output sample space: {event 1, event 2}. This output is then only a part of the input for expectation value function. Event naming is arbitrary, probability only cares about the count or ratio of their occurrences.

You can use the concept of a random variable to assign numbers to the outcome.

http://en.wikipedia.org/wiki/Random_variable
http://www.stat.yale.edu/Courses/1997-98/101/ranvar.htm

Expectation value is measure of probabilities between four possible events. Probabilities naturally range from 0.0 to 1.0, so the reason why expectation values range from -1.0 to +1.0 is because: $E(a,b) = P_{++}(a,b) + P_{--}(a,b) − P_{+-}(a,b) − P_{-+}(a,b)$.

The expectation value of a function of a random variable $f(x)$ is $E(f(x)) = \int f(x) p(x) dx$. In general expectation values do not range between -1 and 1. However, if $f(x)$ ranges between -1 and 1, then the expectation $E(f(x)) = \int f(x) p(x) dx$ also ranges between -1 and 1.

http://mathworld.wolfram.com/ExpectationValue.html

 

[Avodyne]

OK, then we can write

$$P_{++}(a,b)=\int_{\underline{A}(a,\lambda)=+1,\;\underline{B}(b,\lambda)=+1}\rho(\lambda)d\lambda$$

and similarly for $P_{+-}(a,b)$, etc. This notation means that we do the integral only over those values of $\lambda$ for which both $\underline{A}(a,\lambda)=+1$ and $\underline{B}(b,\lambda)=+1$. Here I am adopting the convention that the two binary results are called $+1$ and $-1$. This convention gives us a notation that is useful, in the following sense: the outcomes $++$ and $--$ occur if and only if $\underline{A}(a,\lambda)\underline{B}(b,\lambda)=+1$, and that the outcomes $+-$ and $-+$ occur if and only if $\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1$. Therefore

$$P_{++}(a,b)+P_{--}(a,b) = \int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=+1}\rho(\lambda)d\lambda$$
$$P_{+-}(a,b)+P_{-+}(a,b) = \int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1}\rho(\lambda)d\lambda$$

Now, using $E(a,b)=P_{++}(a,b)+P_{--}(a,b)-P_{+-}(a,b)-P_{-+}(a,b)$, we have

$$E(a,b)=\int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=+1}\rho(\lambda)d\lambda -\int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1}\rho(\lambda)d\lambda$$

Now comes the magic trick:

$$\int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=+1}\rho(\lambda)d\lambda -\int_{\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1}\rho(\lambda)d\lambda =\int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda$$

You must stare at this until you understand it. It is the key to everything. The point is that the factor of $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ on the right-hand side takes on the values $+1$ or $-1$ only (because of the convention that we have adopted). When $\underline{A}(a,\lambda)\underline{B}(b,\lambda)=+1$, we get the first term on the left-hand side, and when $\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1$, we get the second term on the left-hand side.

I'll pause again. I'm hoping that I have now convinced you that, if we adopt the convention that the two binary values are $+1$ and $-1$, then we can write

$$E(a,b)=\int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda$$

 

[Alien8]

However, if $f(x)$ ranges between -1 and 1, then the expectation $E(f(x)) = \int f(x) p(x) dx$ also ranges between -1 and 1.

Binary state events have no range, it's either one or the other. To calculate probabilities and expectation values it is irrelevant whether detections on the two detectors are marked with -1 and +1, or heads and tails. P(+1 and +1) can mean the same thing as P(heads and heads) if we choose so. The things inside probability function brackets are not numbers, but letters. Numbers arithmetic does not directly translate to logic operations of boolean algebra and probabilities.

Do you really mean to say if we decided to mark recordings of the two detectors with heads and tails instead of -1 and +1 the expectation value would range from heads to tails instead of from -1.0 to +1.0?

 

[Alien8]

...occur if and only if $\underline{A}(a,\lambda)\underline{B}(b,\lambda)=-1$.

Why do you think you can multiply "photon A went left" with "photon B went right"?

I'll pause again. I'm hoping that I have now convinced you that, if we adopt the convention that the two binary values are $+1$ and $-1$, then we can write E(a,b)=∫A(a,λ)B(b,λ)ρ(λ)dλ

The integral doesn't imply multiplication of the two terms, but pairing, enumeration and counting.

 

[Nugatory]

Binary state events have no range, it's either one or the other.

Alien8, you are again starting to argue instead of trying to learn. What you should be taking away from the last few posts is that you will have to learn a bit more probability theory before you'll be ready to work through the CHSH derivation and proof.

 

[Nugatory]

Binary state events have no range, it's either one or the other. ... Numbers arithmetic does not directly translate to logic operations of boolean algebra and probabilities.

You are right that discrete ("binary" is a special case of "discrete") outcomes don't have a range. However, we're talking about the expectation value of the result of series of such measurements, and that does have a range. Indeed, that's how casinos stay in business - every spin of the roulette wheel produces a discrete win-lose result for each bet, but the casino knows the exact expectation value of their winnings over a large number of such events, and it approaches a continuous function as the number of events becomes large.

In the Bell and CHSH experiments, the "correlation" values that appear in the formulas are all some form of $(N_1-N_2)/(N_1+N_2)$ where $N_1$ and $N_2$ are the number of trials in which both detectors gave the same result and the number of trials in which both detectors give different results. It should be clear that the expectation value of this quantity can take on values betwen -1 and 1, even though each individual trial has a binary result.

 

[Alien8]

Alien8, you are again starting to argue instead of trying to learn. What you should be taking away from the last few posts is that you will have to learn a bit more probability theory before you'll be ready to work through the CHSH derivation and proof.

I think the misunderstanding is about how the integral works and the meaning of the term $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ when separated out of this expression: $E(a,b)=\int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda$.Alain Aspect paper:
http://arxiv.org/abs/quant-ph/0402001

Equation (5):
$E(a,b) = P_{++}(a,b) + P_{--}(a,b) − P_{+-}(a,b) − P_{-+}(a,b)$

Equation (28):
$E(a,b) = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$I'd say these two equations make it pretty clear the two terms $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ are not multiplied under that integral, but paired and counted. It's not a pair of integers, it's not a pair of probabilities, it's a pair of events. Isn't that true?

 

[wle]

I'd say these two equations make it pretty clear the two terms $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ are not multiplied under that integral, but paired and counted. It's not a pair of integers, it's not a pair of probabilities, it's a pair of events. Isn't that true?

You aren't making much sense. The quantities appearing in the Bell correlator are the combinations of probabilities $$E_{xy} = P_{++}(xy) - P_{+-}(xy) - P_{-+}(xy) + P_{--}(xy) \,.$$ You can, of course, call the binary results anything you want. A common choice is to call them $A_{x} = +1, -1$ and $B_{y} = +1, -1$. This is pure convention, but it's a very nice convention because it makes the combination of probabilities above is the same thing as the expectation value $\langle A_{x} B_{y} \rangle$ of the product of the random variables $A_{x}$ and $B_{y}$. You can't multiply events, but you can certainly multiply the values of variables that you associate to those events, make predictions about their expectation values, and so on.

 

[Alien8]

You aren't making much sense. The quantities appearing in the Bell correlator are the combinations of probabilities $$E_{xy} = P_{++}(xy) - P_{+-}(xy) - P_{-+}(xy) + P_{--}(xy) \,.$$

Please be specific what is not clear and how is what you said different than what I said.

$E(a,b) = \int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$

Do you see right hand side is the result of A(a,λ) and B(b,λ) terms being multiplied under the integral, or being paired and counted to belong in one of the four possible combinations sets?

 

[Alien8]

You can't multiply events, but you can certainly multiply the values of variables that you associate to those events, make predictions about their expectation values, and so on.

Please point some reference about the equation you are talking about. That two coins can either flip heads or tails has no bearing on how often they will both turn on the same side. It means that expectation value: E(a,b) = ∫A(a,λ)B(b,λ)ρ(λ)dλ is not relative or proportional to its input domain limit $\{++, --, +-, -+\}$, which is always the same for every theory and every experiment, but it depends only on hidden variable λ.

 

[wle]

Please be specific what is not clear and how is what you said different than what I said.

$E(a,b) = \int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$

Do you see right hand side is the result of A(a,λ) and B(b,λ) terms being multiplied under the integral, or being paired and counted to belong in one of the four possible combinations sets?

Huh? You estimate $E_{xy}$ in an experiment based on the detection counts $N_{++}(x, y)$ and so on. It is a hypothesis, introduced by Bell and motivated by reasoning about relativistic causality, that $E_{xy}$ should have a theoretical value of the form $$E_{xy} = \int \mathrm{d}\lambda \, \rho(\lambda) \, A_{x}(\lambda) B_{y}(\lambda) \,. \qquad (1)$$ That is what is being tested in a Bell experiment. You don't seem to have understood this. The point of a Bell experiment is to try to show that the assumption (1) is wrong.

 

[wle]

It means that expectation value: E(a,b) = ∫A(a,λ)B(b,λ)ρ(λ)dλ is not relative or proportional to its input domain limit $\{++, --, +-, -+\}$, which is always the same for every theory and every experiment, but it depends only on hidden variable λ.

You are not making any sense at all here.

 

[Alien8]

You are not making any sense at all here.

Please be specific what part is not clear and why. Input domain of A(a,λ) and B(b,λ) for the integral ∫A(a,λ)B(b,λ)ρ(λ)dλ is always the same {++,−−,+−,−+} for every theory and every experiment, yes? Thus the difference between expectation values predicted by different theories is proportional or depends only on hidden variable λ, no?

You estimate Exy in an experiment based on the detection counts N++(x,y) and so on. It is a hypothesis,

$E(a,b) = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$

It's not hypothesis, it's how expectation values is practically calculated, it's simply how expectation value looks naked without the integral. Counts ratio is just another way to express probabilities, it's the same equation as this: $E(a,b) = P_{++}(a,b) + P_{--}(a,b) − P_{+-}(a,b) − P_{-+}(a,b)$.

 

[atyy]

I think the misunderstanding is about how the integral works and the meaning of the term $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ when separated out of this expression: $E(a,b)=\int \underline{A}(a,\lambda)\underline{B}(b,\lambda)\rho(\lambda)d\lambda$.Alain Aspect paper:
http://arxiv.org/abs/quant-ph/0402001

Equation (5):
$E(a,b) = P_{++}(a,b) + P_{--}(a,b) − P_{+-}(a,b) − P_{-+}(a,b)$

Equation (28):
$E(a,b) = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$I'd say these two equations make it pretty clear the two terms $\underline{A}(a,\lambda)\underline{B}(b,\lambda)$ are not multiplied under that integral, but paired and counted. It's not a pair of integers, it's not a pair of probabilities, it's a pair of events. Isn't that true?

There are different ways of doing it, and also different people use the same words for different things, and different words for the same things. Wikipedia does CHSH in two different ways, and Alain Aspect does it yet another way. They are all correct (except maybe the reference to the triangle inequality by Wikipedia, which I don't understand). Anyway, if you want to stick to the derivation in the paper by Alain Aspect, that is a fine way to learn CHSH.

 

[Alien8]

There are different ways of doing it, and also different people use the same words for different things, and different words for the same things. Wikipedia does CHSH in two different ways, and Alain Aspect does it yet another way. They are all correct (except maybe the reference to the triangle inequality by Wikipedia, which I don't understand). Anyway, if you want to stick to the derivation in the paper by Alain Aspect, that is a fine way to learn CHSH.

Yes, I'd rather get back to my original question.

I'd like see how this equation in step (6) looks like without step (5) applied to it in terms of expectation values. So given:

∫A(a,λ)B(b,λ)ρ(λ)dλ = E(a,b)
∫A(a,λ)B(b′,λ)ρ(λ)dλ = E(a,b′)
∫A(a′,λ)B(b′,λ)ρ(λ)dλ = E(a′,b′)
∫A(a′,λ)B(b,λ)ρ(λ)dλ = E(a′,b)

...and without the insertion of +/- 1, does step (6) not boil down to this: E(a,b) - E(a,b') = E(a,b) * E(a',b') - E(a,b') * E(a',b)?

 

[wle]

Please be specific what part is not clear and why.

You are writing in a language I've never seen before. I don't know what you're calling an "input domain limit", what it means for an integral to "have" or be "relative" or "proportional" to an "input domain limit", or why you think it's true for every theory and every experiment.

$E(a,b) = \frac {N_{++}(a,b) + N_{--}(a,b) - N_{+-}(a,b) - N_{-+}(a,b)} {N_{++}(a,b) + N_{--}(a,b) + N_{+-}(a,b) + N_{-+}(a,b)}$

It's not hypothesis

$E(x, y) = \int \mathrm{d}\lambda \, \rho(\lambda) \, A_{x}(\lambda) B_{y}(\lambda)$ is the hypothesis.

 

[Alien8]

You are writing in a language I've never seen before. I don't know what you're calling an "input domain limit", what it means for an integral to "have" or be "relative" or "proportional" to an "input domain limit", or why you think it's true for every theory and every experiment.

- the domain of a function is the set of "input" or argument values for which the function is defined
http://en.wikipedia.org/wiki/Domain_of_a_function

- the sample space of an experiment or random trial is the set of all possible outcomes or results of that experiment
http://en.wikipedia.org/wiki/Sample_space

E(a,b) = ∫A(a,λ)B(b,λ)ρ(λ)dλ

1. outcome sample space for A(a,λ) and B(b,λ) integral pairs is always S = {++,−−,+−,−+}
2. sample space {++,−−,+−,−+} is thus the input domain for the integral ∫A(a,λ)B(b,λ)ρ(λ)dλ
3. 1 and 2 are true for every CHSH experiment and for every theory whether local or non-local
4. different theories predict different expectation values for E(a,b) given the same a and b
5. the difference between proposed E(a,b) functions is relative only to λ and not S = {++,−−,+−,−+}

$E(x, y) = \int \mathrm{d}\lambda \, \rho(\lambda) \, A_{x}(\lambda) B_{y}(\lambda)$ is the hypothesis.

That's a description of expectation value in terms of hidden variable λ. The other one is the description in terms of probabilities. Neither are hypothetical, they are just algebraic. Hypothesis is E(x, y) = cos2(x-y), which just happens to be true, for some reason.

 

[wle]

- the domain of a function is the set of "input" or argument values for which the function is defined
http://en.wikipedia.org/wiki/Domain_of_a_function

2. sample space {++,−−,+−,−+} is thus the input domain for the integral ∫A(a,λ)B(b,λ)ρ(λ)dλ

No, that doesn't make sense, because the integral is not a function. Even if you recast it as a function, its inputs would be the whole functions $A_{x}(\lambda)$ and $B_{y}(\lambda)$. It is not a function of ++, +-, -+, or --.

3. 1 and 2 are true for every CHSH experiment and for every theory whether local or non-local

That also doesn't make sense. $\int \mathrm{d}\lambda \, \rho(\lambda) \, A_{x}(\lambda) B_{y}(\lambda)$ is the expectation value for local theories only.

That's a description of expectation value in terms of hidden variable λ.

The hidden variable is hypothetical. We do not measure $\lambda$ in an experiment. We don't know that a $\lambda$ even exists at all.

Hypothesis is E(x, y) = cos2(x-y), which just happens to be true, for some reason.

No, that has been confirmed in experiments. That is not hypothetical.

 

[Nugatory]

-
That [the integral defining $E(x,y)$] is a description of expectation value in terms of hidden variable λ. The other one is the description in terms of probabilities. Neither are hypothetical, they are just algebraic

That integral is a calculation of the expectation value in terms of probabilities, under the hypothesis that the probabilities take a particular form. That hypothetical form makes them out to be functions of $\lambda$ and $x$ on one side, and $\lambda$ and $y$ on the other, but the appearance of $\lambda$ in the integral doesn't mean that this is somehow not an expression in terms of probabilities. Yes, the calculation is "just algebraic", but it's "just algebra" proceeding from the hypothesis, which is not:

Hypothesis is E(x, y) = cos2(x-y), which just happens to be true, for some reason.

No, that is an experimental observation, which just happens to be predicted by quantum mechanics. That observation also conflicts with the hypothesis above about the form of the probabilities.

 

[atyy]

Yes, I'd rather get back to my original question.

I'd like see how this equation in step (6) looks like without step (5) applied to it in terms of expectation values. So given:

∫A(a,λ)B(b,λ)ρ(λ)dλ = E(a,b)
∫A(a,λ)B(b′,λ)ρ(λ)dλ = E(a,b′)
∫A(a′,λ)B(b′,λ)ρ(λ)dλ = E(a′,b′)
∫A(a′,λ)B(b,λ)ρ(λ)dλ = E(a′,b)

...and without the insertion of +/- 1, does step (6) not boil down to this: E(a,b) - E(a,b') = E(a,b) * E(a',b') - E(a,b') * E(a',b)?

No, including the +/- 1 it is

$E(a,b) - E(a,b') = \int[D1 - D2]\rho(\lambda)d\lambda = ∫[D1 - D2 + D1*D3 + D1*D3]\rho(\lambda)d\lambda$

where D1, D2, D3, D4 were defined in post #6.

 

[Alien8]

No, that doesn't make sense, because the integral is not a function. Even if you recast it as a function, its inputs would be the whole functions $A_{x}(\lambda)$ and $B_{y}(\lambda)$. It is not a function of ++, +-, -+, or --.

Would you please rather try to answer my question in post #29? Can you confirm what atty wrote above?

 

[Alien8]

No, including the +/- 1 it is

$E(a,b) - E(a,b') = \int[D1 - D2]\rho(\lambda)d\lambda = ∫[D1 - D2 + D1*D3 + D1*D3]\rho(\lambda)d\lambda$

where D1, D2, D3, D4 were defined in post #6.

Can we exclude step (5) and write the equation (6) without including +/- 1?Is $E(a,b) - E(a,b') = \int[D1 - D2]\rho(\lambda)d\lambda$ not the same thing as $E(a,b) - E(a,b') = E(a,b) - E(a,b')$?In terms of D variables:

A(a,λ)B(b,λ) = D1
A(a,λ)B(b′,λ) = D2
A(a′,λ)B(b′,λ) = D3
A(a′,λ)B(b,λ) = D4

this right hand side of the step (6):

goes like this:
$\int D1[1 \pm D3 ] - \int D2[1 \pm D4 ]$?

Can we not just pull that $1 \pm$ straight out of it? How did that +/- 1 even got there, what kind of mathematics is that?