bagasme
- 79
- 9
Hello,
Here in this thread I will derive formulas for relation between two wheels, either teethed (e.g. gears) or non-teethed.
In wheel relationship, we have three cases:
1. At the same axle
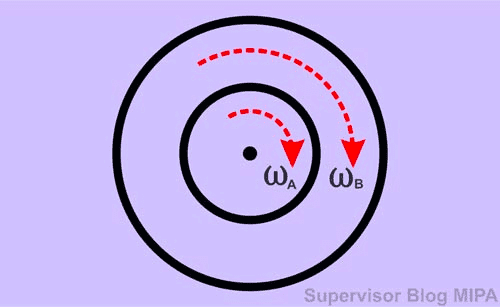
Figure 1 (source: fisikabc.com) shows two wheels connected to the same axle. Since both ##A## and ##B## are on same center, they have same angular accelleration:
$$\begin{align}
\omega_A & = \omega_B \nonumber \\
\frac {v_A} {r_A} & = \frac {v_B} {r_B} ~ (1)\nonumber
\end{align}$$
2. Intersected in Parallel
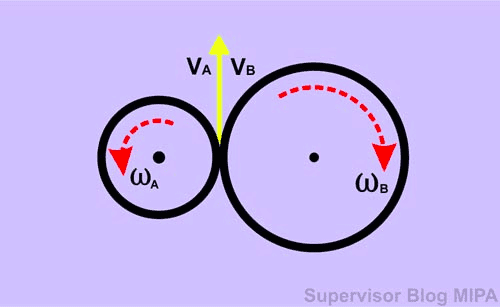
Figure 2 (source: fisikabc.com) show two wheels intersected each other in parallel. When wheel ##A## rotated counter-clockwise, wheel ##B## rotated clockwise, and vice versa. At the intersection point between two wheels, linear velocity of both wheels directed at the same direction, so:
$$\begin{align}
v_A & = v_B \nonumber \\
\omega_A \cdot r_A &= \omega_B \cdot r_B ~ (2)\nonumber
\end{align}$$
3. Connected by Belt
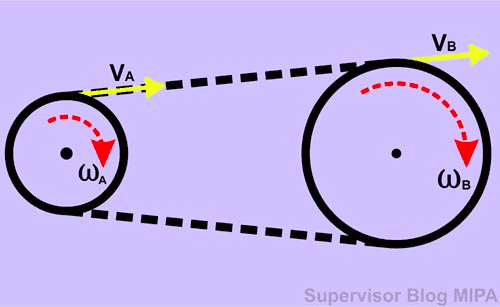
Figure 3 (source: fisikabc.com) shows two wheels connected by a belt. As wheel ##B## rotated, the belt rotated wheel ##A## at the same linear velocity direction as wheel ##B##. Thus the formula is same as when both wheels intersected directly (2).
Relationship Involving Teethed Wheels (e.g. Gears)
We will now deriving equations that relate between angular velocity, radius, and number of teeth. ##N_A## and ##N_B## are number of teeth of wheel A and B, respectively.
From equation (2):
$$\begin{align}
\omega_A \cdot r_A & = \omega_B \cdot r_B \nonumber \\
\frac {2 \cdot \pi \cdot r_A} {t} & = \frac {2 \cdot \pi \cdot r_B} {t} \nonumber \\
r_A &= r_B \nonumber \\
\frac {r_A} {n_A} &= \frac {r_B} {n_B} \nonumber \\
r_A \cdot N_B &= r_B \cdot N_A \nonumber \\
\frac {r_A} {r_B} &= \frac {N_A} {N_B} ~ (3) \nonumber
\end{align}$$
Combining equation (2) and (3):
$$\begin{align}
\omega_A \cdot r_A & = \omega_B \cdot r_B \nonumber \\
\frac {\omega_A} {\omega_B} &= \frac {r_B} {r_A} \nonumber \\
\frac {\omega_A} {\omega_B} &= \frac {N_B} {N_A} \nonumber \\
\end{align}$$
We can conclude that angular accelleration is related to radius, but inverse related to number of teeth.
I hope that this thread will be useful. Please let me know any flaws and suggestions.
Cheers, Bagas
Here in this thread I will derive formulas for relation between two wheels, either teethed (e.g. gears) or non-teethed.
In wheel relationship, we have three cases:
- Two wheels at the same axle
- Two wheels intersected in parallel (meshed)
- Two wheels connected by a belt
1. At the same axle
Figure 1 (source: fisikabc.com) shows two wheels connected to the same axle. Since both ##A## and ##B## are on same center, they have same angular accelleration:
$$\begin{align}
\omega_A & = \omega_B \nonumber \\
\frac {v_A} {r_A} & = \frac {v_B} {r_B} ~ (1)\nonumber
\end{align}$$
2. Intersected in Parallel
Figure 2 (source: fisikabc.com) show two wheels intersected each other in parallel. When wheel ##A## rotated counter-clockwise, wheel ##B## rotated clockwise, and vice versa. At the intersection point between two wheels, linear velocity of both wheels directed at the same direction, so:
$$\begin{align}
v_A & = v_B \nonumber \\
\omega_A \cdot r_A &= \omega_B \cdot r_B ~ (2)\nonumber
\end{align}$$
3. Connected by Belt
Figure 3 (source: fisikabc.com) shows two wheels connected by a belt. As wheel ##B## rotated, the belt rotated wheel ##A## at the same linear velocity direction as wheel ##B##. Thus the formula is same as when both wheels intersected directly (2).
Relationship Involving Teethed Wheels (e.g. Gears)
We will now deriving equations that relate between angular velocity, radius, and number of teeth. ##N_A## and ##N_B## are number of teeth of wheel A and B, respectively.
From equation (2):
$$\begin{align}
\omega_A \cdot r_A & = \omega_B \cdot r_B \nonumber \\
\frac {2 \cdot \pi \cdot r_A} {t} & = \frac {2 \cdot \pi \cdot r_B} {t} \nonumber \\
r_A &= r_B \nonumber \\
\frac {r_A} {n_A} &= \frac {r_B} {n_B} \nonumber \\
r_A \cdot N_B &= r_B \cdot N_A \nonumber \\
\frac {r_A} {r_B} &= \frac {N_A} {N_B} ~ (3) \nonumber
\end{align}$$
Combining equation (2) and (3):
$$\begin{align}
\omega_A \cdot r_A & = \omega_B \cdot r_B \nonumber \\
\frac {\omega_A} {\omega_B} &= \frac {r_B} {r_A} \nonumber \\
\frac {\omega_A} {\omega_B} &= \frac {N_B} {N_A} \nonumber \\
\end{align}$$
We can conclude that angular accelleration is related to radius, but inverse related to number of teeth.
I hope that this thread will be useful. Please let me know any flaws and suggestions.
Cheers, Bagas