Tony Hau
- 107
- 30
In my textbook, the effective force of a particle on a rotating frame is given as below:
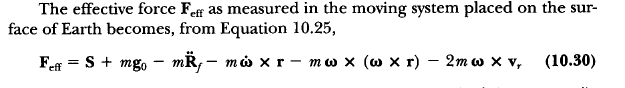
The diagram is:
What I do not understand is the expression for Rf dotdot, which is given as below:

According to the book, an arbitary vector Q can be expressed as:

So Rdotdot w.r.t fixed frame can be obtained by substituting Q for Rdot
Why the Rdotdot w.r.t. the rotating frame is gone when we derive (10.31) from (10.12)? As the frame is moving away from the centre of Earth, the R, which is the distance between the frame and the centre of the Earth, should be changing as well when measured from the moving frame.
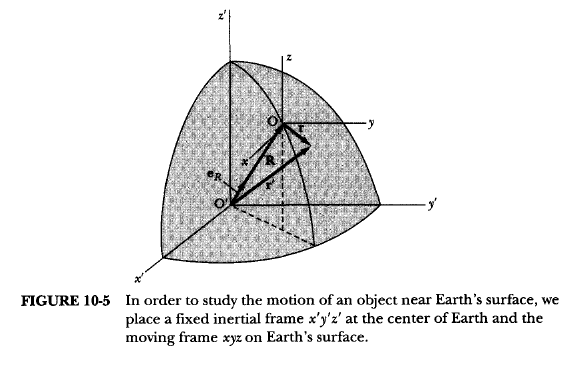
The diagram is:
What I do not understand is the expression for Rf dotdot, which is given as below:
According to the book, an arbitary vector Q can be expressed as:
So Rdotdot w.r.t fixed frame can be obtained by substituting Q for Rdot
Why the Rdotdot w.r.t. the rotating frame is gone when we derive (10.31) from (10.12)? As the frame is moving away from the centre of Earth, the R, which is the distance between the frame and the centre of the Earth, should be changing as well when measured from the moving frame.
Last edited: