Derive the equation of effective force on a rotating frame about Earth

[Tony Hau]

In my textbook, the effective force of a particle on a rotating frame is given as below:

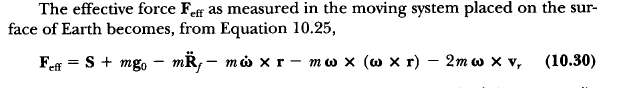
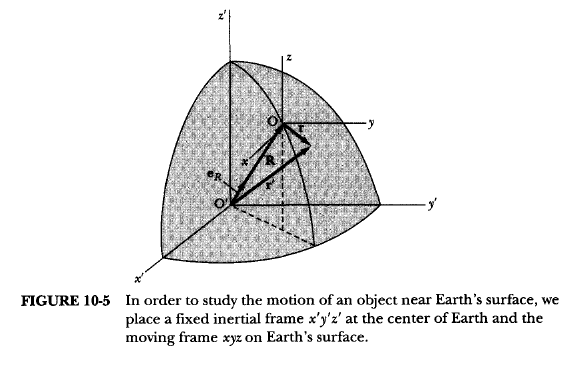
The diagram is:

What I do not understand is the expression for Rf dotdot, which is given as below:

According to the book, an arbitary vector Q can be expressed as:

So Rdotdot w.r.t fixed frame can be obtained by substituting Q for Rdot

Why the Rdotdot w.r.t. the rotating frame is gone when we derive (10.31) from (10.12)? As the frame is moving away from the centre of Earth, the R, which is the distance between the frame and the centre of the Earth, should be changing as well when measured from the moving frame.

 

[Tony Hau]

I just figure out the answer. I think it is because the frame is not moving with respect to the centre of the Earth. It is the object, whose distance from the moving frame is denoted as small letter r, that is changing. So the time derivative of R with respect to the rotating frame is not changing. The frame is only rotating around the Earth and so the time derivative with respect to the fixed Earth frame is omega cross r.