SUMMARY
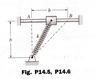
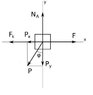
The discussion focuses on deriving the expression for the work done by the friction force on a slider moving from point A to point B, with a coefficient of kinetic friction denoted as μ. Key equations include the normal force equation, N_A = P cos(φ), and the force balance equations ΣFx=0 and ΣFy=0. The participants emphasize the need to express the spring tension P as a function of the angle φ and to analyze the forces at various points along the path. The final expression for P at point B is determined to be -0.414kb, where k is the spring constant.
PREREQUISITES
- Understanding of kinetic friction and its coefficient (μ)
- Knowledge of force balance equations in mechanics (ΣFx and ΣFy)
- Familiarity with spring mechanics and Hooke's Law (P = -kx)
- Ability to apply trigonometric functions in physics problems (sin and cos functions)
NEXT STEPS
- Learn how to derive expressions for forces in dynamic systems using Free Body Diagrams (FBD)
- Study the integration of functions to calculate work done by variable forces
- Explore the relationship between angle and force in spring systems
- Investigate the application of Pythagorean theorem in mechanics for distance calculations
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and dynamics, as well as educators seeking to enhance their understanding of friction and spring systems in practical applications.