meyol99
- 25
- 1
Hello everybody,
I have a new thread to post,it is very important to find a solution for this :
-Imagine a box full of air particles.The particles are forced to move to a point A on the edge of the box.My question is now,how can I mathematicly describe the movement of these particles toward point A using one generalised equation ?
(See picture.)
Thank you for your time.
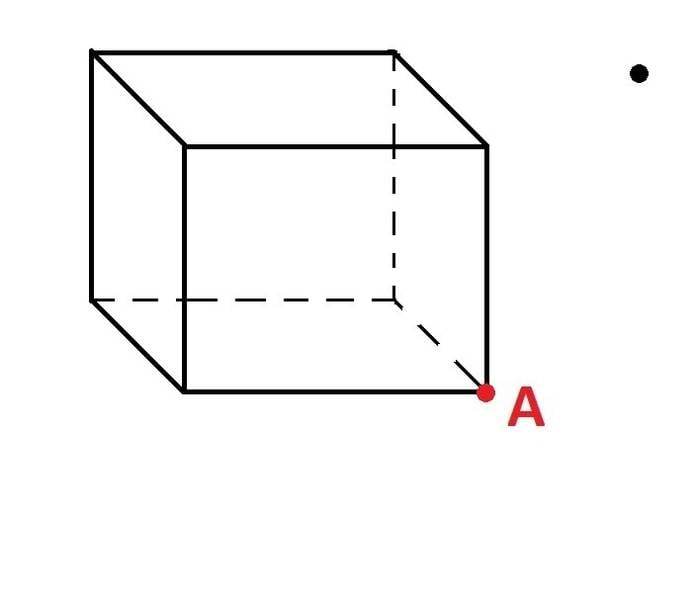
I have a new thread to post,it is very important to find a solution for this :
-Imagine a box full of air particles.The particles are forced to move to a point A on the edge of the box.My question is now,how can I mathematicly describe the movement of these particles toward point A using one generalised equation ?
(See picture.)
Thank you for your time.