Describing path of the object in an xy plane

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For part(d) of this problem,

The solution is,

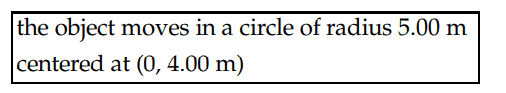
However, how did they know that the object moves in a circle of radius 5.00m centered at (0,4.00m)?

Many thanks!

 

[kuruman]

What is the equation of a circle centered at $(x_0,y_0)$?

 

[nasu]

The coordinates satisfy the equation of such a circle. This is how they know.

 

[member 731016]

Thank you for your replies @kuruman and @nasu!

The equation of a circle centered at $(x_0, y_0)$ is $(x - x_0)^2 + (y - y_0)^2 = r^2$

Many thanks!

 

[kuruman]

Can you bring what you have in that form? Remember that $~\sin^2x+\cos^2x=1.$

 

[member 731016]

Can you bring what you have in that form? Remember that $~\sin^2x+\cos^2x=1.$

Thank you for your reply @kuruman !

Here is what I got:

$x^2 + y^2 = r^2$
$(-5.00sin\omega t)^2 + (4.00 - 5cos\omega t)^2 = r^2$
$25sin^2\omega t + 16 - 40cos\omega t +25cos^2\omega t = r^2$
$25(sin^2\omega t + cos^2\omega t) +16 - 40cos\omega t = r^2$
$41 - 40cos\omega t = r^2$

EDIT: I'm now thinking that I should put the individual position function in the x-components in the y-components in the circle formula I posted.

Many thanks!

 

[MatinSAR]

Here is what I got:

Don't try to prove that way ...

EDIT: I'm now thinking that I should put the individual position function in the x-components in the y-components in the circle formula I posted.

Yes.
We know that $x=-5sinωt$ and $y-4=-5cosωt$ so we have:
$x^2+(y-4)^2=25sin^2ωt+25cos^2ωt=25$ and we know that $x^2+(y-4)^2=5^2$ is equation of a circle with $r=5$ that is centered at $(0,4)$.

 

[member 731016]

Don't try to prove that way ...

Yes.
We know that $x=-5sinωt$ and $y-4=-5cosωt$ so we have:
$x^2+(y-4)^2=25sin^2ωt+25cos^2ωt=25$ and we know that $x^2+(y-4)^2=5^2$ is equation of a circle with $r=5$ that is centered at $(0,4)$.

Thank you for your reply @MarinSAR! I see now :)