Designing a 2-bit full adder using nothing but NAND gates?
Click For Summary
Discussion Overview
The discussion revolves around designing a 2-bit full adder using only NAND gates. Participants explore the feasibility of minimizing the number of logic gates while adhering to the constraints of using NAND gates exclusively. The conversation includes technical details about circuit design, logic gate functions, and potential simplifications.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
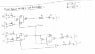
- One participant presents their design for a 2-bit full adder and seeks advice on reducing the number of logic gates.
- Another participant questions the carry output (Cout) in the design, suggesting it may always be on if a certain input is zero.
- Several participants discuss the necessity of using Karnaugh maps for minimizing logical expressions and converting them to NAND gate configurations.
- One participant mentions that a 2-bit full adder requires a carry input to function as a full adder, highlighting the need for clarity on the design's specifications.
- A participant proposes a method to construct 3-input EXOR and MAJORITY gates using only 2-input NAND gates, suggesting a potential design that requires fewer gates.
- Another participant suggests that the design presented does not constitute a full 2-bit adder due to the absence of a carry input, indicating that it may only function as a half adder.
Areas of Agreement / Disagreement
Participants express differing views on the design's validity as a full adder and the necessary components for a complete 2-bit adder. There is no consensus on the optimal design or the minimum number of gates required, as various approaches and corrections are proposed throughout the discussion.
Contextual Notes
Participants note that the design is constrained to using only 2-input NAND gates and that the challenge does not specify a target technology beyond using 7400 integrated circuits. The discussion also highlights the importance of understanding the rules of the challenge, including whether a carry input is required for the first stage.
Similar threads
- · Replies 5 ·
- · Replies 3 ·
- · Replies 6 ·
- · Replies 3 ·
- · Replies 4 ·
- · Replies 6 ·
- · Replies 16 ·