Desorption probability calculation

[CloudNine]

Hi all!

I would like your assistance with wrapping up my thoughts regarding the following problem.

Say I have Am-241 nuclide, which emits alpha particle in every decay (for the sake of this discussion, let's assume that 100% of the decays lead to a daughter nuclide, Np-237 + an alpha particle). Let's consider the following setups (see picture below):

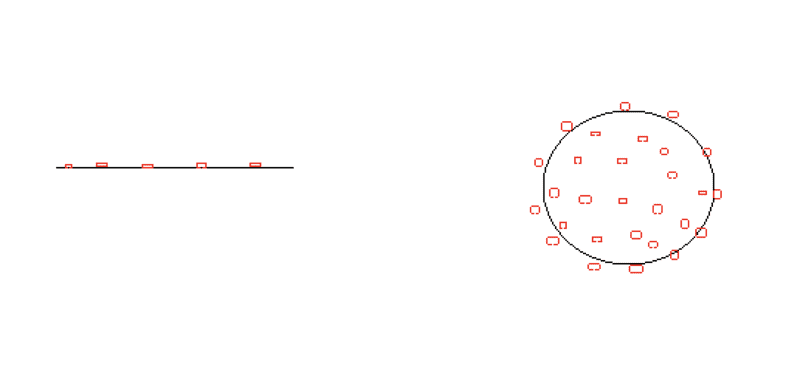
On the left hand side, I have a rod (a side view), with a certain thickness, with Am-241 atoms (represented by the red hollow circles) attached to one side of it.
On the right hand side, I have a solid cylinder (a cross section), with Am-241 atoms evenly distributed along the entire volume & surface of the cylinder.
Now, If I would like to calculate the desorption probability of Np-237 (meaning, the probability for Np-237 release from the rod/cylinder into the air, for each decay of Am-241), the left case it is quite straight forward, as there's 50% chance that the Np-237 atom will recoil out of the rod and 50% chance that the Np-237 atom will recoil into the rod (lets say that the Np-237's energy isn't high enough to pass through the rod's thickness and leave it on the other side).

How would I calculate the desorption probability of Np-237 on the second case? Basically, the atoms on the cylinder's surface also have a 50% percent chance to leave the surface, but what about the atoms confined within the volume? How can I mathematically describe the probabilities there?

Would appreciate your assistance :)

Thanks!

 

[Astronuc]

Say I have Am-241 nuclide, which emits alpha particle in every decay (for the sake of this discussion, let's assume that 100% of the decays lead to a daughter nuclide, Np-237 + an alpha particle).

A reasonable assumption. This is a real issue for alpha emitters, since individual atoms can be knocked of the surface, and if oxygen is present, the atoms can react and become oxide molecules and be airborne. This is why appropriate storage is critical. It's more likely though that He will accumulate on the grain boundaries of the material, and eventually, grains of the material will pop out of the surface, and become airborne particles.

The α-decay energies are 5.486 MeV for 85% of the time (the one which is widely accepted for standard α-decay energy), 5.443 MeV for 13% of the time, and 5.388 MeV for the remaining 2%.
Ref: https://en.wikipedia.org/wiki/Americium-241 (link to original source no longer available)

The recoil energy of the Np-237 atom is about 5.486 * (4/237) ~ 0.0926 Mev = 92.6 keV

In the two examples, one seems to be considering a two surface (very thin layers) vs a thicker volume presenting one surface. Is this correct?

So, the probability of a Np-237 getting knocked out per unit surface is about the same. Either Np-237 can directly recoil off the surface, or an alpha particle can knock an Am-241 or Np-237 atom of the surface.

See - Alpha-Recoil and Fission Fragment Induced Desorption of Secondary Ions
https://link.springer.com/chapter/10.1007/978-3-642-61871-0_84

Consider purchasing the book - https://link.springer.com/book/10.1007/978-3-642-61871-0
See - Atom Ejection Mechanisms and Models, Don E. Harrison Jr., Barbara J. Garrison, Nicholas Winograd, pp. 12-14

Alternatively, see K.Wien, O.Becker, P.Daab, D.Nederveld, "Experimental investigation of fission fragment and alpha-recoil induced ejection of secondary ions," Nuclear Instruments and Methods, Volume 170, Issues 1–3, 15 March 1980, Pages 477-481

See discussion under - Material Properties/Oxide Fuels for Light Water Reactors and Fast Neutron Reactors, T. Wiss, in Comprehensive Nuclear Materials, 2012
https://www.sciencedirect.com/topics/physics-and-astronomy/alpha-decay

a heavy recoil atom, for example, 237Np in the decay of 241Am which receives a recoil energy E due to conservation of momentum, ME = mEα, hence typically ∼100keV (or 91keV in the decay of 241Am).

These recoil atoms show predominantly nuclear stopping and produce a dense collision cascade with typically ∼1500 displacements within a short distance of ∼20nm. Defect clustering can occur, stabilizing the damage.