gtavictor
- 7
- 0
Detailed modeling of a Pulley System, HELP!
Hello people,
Currently I have a project of a pulley system, and I have to model it with fair detailed equations. Actually this continues from another thread I started sometime ago, but I made a new thread because now I'm continuing with the project. The next are the considerations I need to be aware of:
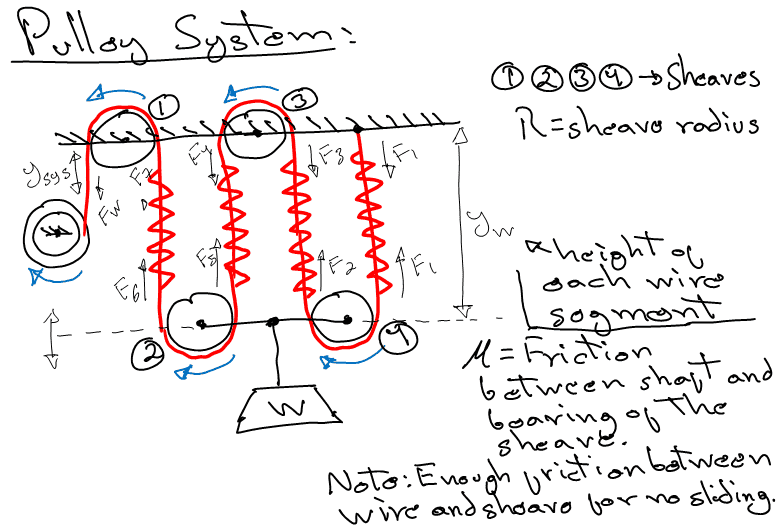
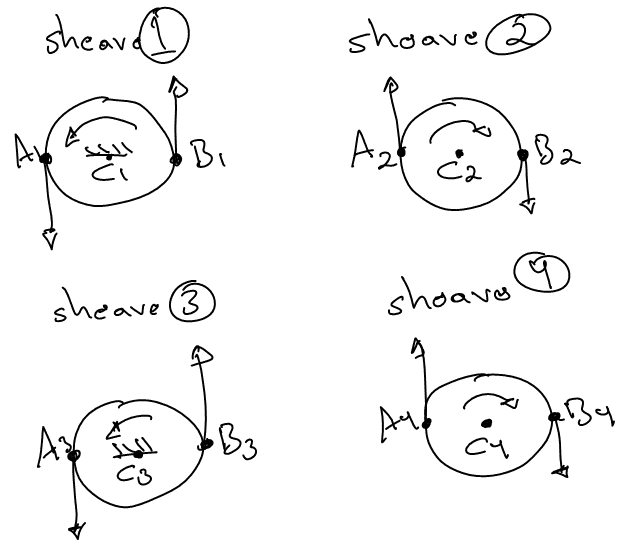
Sheave modeling: For this I'm based on the first and second images. I'm doing the modeling for the velocities, so if I integrate or derivate I get position or acceleration respectively:
Sheave1: in this case v_{c1}=0
v_{a1}=v_{c1}-R*\omega_1=-R*\omega_1
v_{b1}=v_{c1}+R*\omega_1=R*\omega_1
v_{a1}=-v_{b1}
Sheave2:
v_{a2}=v_{c2}-R*\omega_2
v_{b2}=v_{c2}+R*\omega_2
Sheave3: in this case v_{c3}=0
v_{a3}=v_{c3}-R*\omega_3=-R*\omega_3
v_{b3}=v_{c3}+R*\omega_3=R*\omega_3
Sheave4: in this case v_{b4}=0
v_{a4}=v_{c4}-R*\omega_4
v_{b4}=v_{c4}+R*\omega_4 --> v_{c4}=-R*\omega_4
also --> v_{a4}=-2*R*\omega_4
Then I consider the velocities the same where I have one same string connected:
v_{b1}=v_{a2}
v_{b2}=v_{a3}
v_{a4}=v_{b3}
From this sheaves modeling I don't know if these velocities I mentioned before are the same, from the initial considerations I have a stretchable spring but from what I know the velocities in both ends of the wire segment between sheave and sheave should not be the same, if that's the case then, how can I model each sheave individually with different velocities?
Tensions in each wire segment due to friction shaft-bearing: For this I'm based on the first image, starting for the rightest sheave (where less tension should be applied in the wires due to the final fixed point).
r=Radius of shaft
R=Radius of sheave
For sheave 4:
N=T_2+T_1
\mu*N*r=(T_2-T_1)
N=\frac{(T_2-T_1)*R}{\mu*r}
\frac{(T_2-T_1)*R}{\mu*r}-T_1-T_2=0
T_2=\frac{T_1*(R+\mu*r)}{R-\mu*r}
then for sheave 3:
T_4=\frac{T_1*(R+\mu*r)^2}{(R-\mu*r)^2}
then for sheave 2:
T_6=\frac{T_1*(R+\mu*r)^3}{(R-\mu*r)^3}
then for sheave 1:
F_w=\frac{T_1*(R+\mu*r)^4}{(R-\mu*r)^4}
For this modeling I just did I see from the equations that I have an increase of tension due to the friction between shaft and bearing of the sheave, but like for the previous modeling I'm not sure if I'm doing good, also, the tension in 1 should be IDEALLY:
T_1=\frac{W}{MA} where MA is the mechanical advantage equal to 4 for this pulley system, but still this is IDEALLY, so I don't know how to model some good equations for this part, at least I have something.
Moments on sheaves: I did some modeling about the moments present on each sheave and for that I come up with a general equation:
J_o*\ddot{\theta}_n=[(\frac{T_1*(R+\mu*r)^{n-1}}{(R-\mu*r)^{n-1}})-(\frac{T_1*(R+\mu*r)^{n}}{(R-\mu*r)^{n}})]*R-(-1)^{n+1}*\mu*[(\frac{T_1*(R+\mu*r)^{n-1}}{(R-\mu*r)^{n-1}})+(\frac{T_1*(R+\mu*r)^{n}}{(R-\mu*r)^{n}})]*r
where n = sheave number from the first image (not the number or quantity of sheaves)
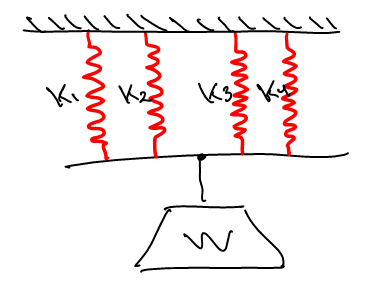
Forces on the Weight: For this modeling I use the third image.
m*a+K_1*y+K_2*y+K_3*y+K_4*y=0
In this case I might consider the stiffness equal in each wire segment but still when I think about this equation I get problems with the others.
Please I nee good help about the detailed modeling of this system, I guess it's complicated from a first point of view but maybe it's because of my lack of knowledge on this kind of modeling!
Thanks in advance!
Hello people,
Currently I have a project of a pulley system, and I have to model it with fair detailed equations. Actually this continues from another thread I started sometime ago, but I made a new thread because now I'm continuing with the project. The next are the considerations I need to be aware of:
- Wire rope as a stretchable string (I suppose I have to model it as a spring).
- Damping in the wire can be neglected but consider a very high stifness of the wire so small permanent oscillations occur in the system.
- Angular position, velocity and acceleration of each sheave.
- Displacement, velocity and position of the sheaves attached to the weight, in this case is obvious both sheaves and the weight share the same translational movements.
- Consider \mu as the friction between shaft and bearing of the sheave.
- Consider the friction between wire rope and sheave high enough so no sliding occurs.
Sheave modeling: For this I'm based on the first and second images. I'm doing the modeling for the velocities, so if I integrate or derivate I get position or acceleration respectively:
Sheave1: in this case v_{c1}=0
v_{a1}=v_{c1}-R*\omega_1=-R*\omega_1
v_{b1}=v_{c1}+R*\omega_1=R*\omega_1
v_{a1}=-v_{b1}
Sheave2:
v_{a2}=v_{c2}-R*\omega_2
v_{b2}=v_{c2}+R*\omega_2
Sheave3: in this case v_{c3}=0
v_{a3}=v_{c3}-R*\omega_3=-R*\omega_3
v_{b3}=v_{c3}+R*\omega_3=R*\omega_3
Sheave4: in this case v_{b4}=0
v_{a4}=v_{c4}-R*\omega_4
v_{b4}=v_{c4}+R*\omega_4 --> v_{c4}=-R*\omega_4
also --> v_{a4}=-2*R*\omega_4
Then I consider the velocities the same where I have one same string connected:
v_{b1}=v_{a2}
v_{b2}=v_{a3}
v_{a4}=v_{b3}
From this sheaves modeling I don't know if these velocities I mentioned before are the same, from the initial considerations I have a stretchable spring but from what I know the velocities in both ends of the wire segment between sheave and sheave should not be the same, if that's the case then, how can I model each sheave individually with different velocities?
Tensions in each wire segment due to friction shaft-bearing: For this I'm based on the first image, starting for the rightest sheave (where less tension should be applied in the wires due to the final fixed point).
r=Radius of shaft
R=Radius of sheave
For sheave 4:
N=T_2+T_1
\mu*N*r=(T_2-T_1)
N=\frac{(T_2-T_1)*R}{\mu*r}
\frac{(T_2-T_1)*R}{\mu*r}-T_1-T_2=0
T_2=\frac{T_1*(R+\mu*r)}{R-\mu*r}
then for sheave 3:
T_4=\frac{T_1*(R+\mu*r)^2}{(R-\mu*r)^2}
then for sheave 2:
T_6=\frac{T_1*(R+\mu*r)^3}{(R-\mu*r)^3}
then for sheave 1:
F_w=\frac{T_1*(R+\mu*r)^4}{(R-\mu*r)^4}
For this modeling I just did I see from the equations that I have an increase of tension due to the friction between shaft and bearing of the sheave, but like for the previous modeling I'm not sure if I'm doing good, also, the tension in 1 should be IDEALLY:
T_1=\frac{W}{MA} where MA is the mechanical advantage equal to 4 for this pulley system, but still this is IDEALLY, so I don't know how to model some good equations for this part, at least I have something.
Moments on sheaves: I did some modeling about the moments present on each sheave and for that I come up with a general equation:
J_o*\ddot{\theta}_n=[(\frac{T_1*(R+\mu*r)^{n-1}}{(R-\mu*r)^{n-1}})-(\frac{T_1*(R+\mu*r)^{n}}{(R-\mu*r)^{n}})]*R-(-1)^{n+1}*\mu*[(\frac{T_1*(R+\mu*r)^{n-1}}{(R-\mu*r)^{n-1}})+(\frac{T_1*(R+\mu*r)^{n}}{(R-\mu*r)^{n}})]*r
where n = sheave number from the first image (not the number or quantity of sheaves)
Forces on the Weight: For this modeling I use the third image.
m*a+K_1*y+K_2*y+K_3*y+K_4*y=0
In this case I might consider the stiffness equal in each wire segment but still when I think about this equation I get problems with the others.
Please I nee good help about the detailed modeling of this system, I guess it's complicated from a first point of view but maybe it's because of my lack of knowledge on this kind of modeling!
Thanks in advance!