Determine function from the graph

[Goodver]

How to determine the function from its graph if it has a non-simple shape?

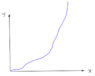
Given a graph (see attachment) where set of coordinates of any point is known. Are there any techniques to find an equation of the function? So far i can guess, that i need to measure the derivative at multiple points, then plot it, then find graph of second derivative and so on until i get a 0 derivative, and then integrate backwards to obtain original equation.

Could anyone please mention whether there are some techniques to perform such evaluations i could read about?

 

[HallsofIvy]

You can't. Theoretically, there exist a unique function having a given graph. Practically, which is what I assume you mean, you can only deal with a finite number of data points and there always exist an infinite number of functions passing through a finite number of given points.

If you can "guess" the type of function, polynomial, exponential, trig, etc (which are really "simple" types of functions) you can write out a "general" form (y= c_nx^n+ c_{n-1}x^{n-1}+\cdot\cdot\cdot+ c_1x+ c_0 or y= ae^{bx} or y= acos(x)+ bsin(x)+ c cos(3x)+ d sin(3x)) and use as many points as you have unknown coefficients to get equations to solve for those coefficients.

Or you can use the fact that any continuous function can be approximated to any degree of accuracy by a polynomial to get an approximation to the function by a, perhaps very, very high degree, polynomial.

It sounds to me like you are trying to use points to approximate the function- though if you have the graph of the function itself I can't imagine why you would "measure the derivative at multiple points" and then integrate when you can approximate the function itself directly.

It sounds like you need to use, say, "Newton's divided difference formula":
http://www.math.ucla.edu/~ronmiech/YAN/ndivdiff.html